什么是齿轮的渐开线

中文名称：渐开线

英文名称：involute

定义：在平面上，一条动直线（发生线）沿着一个固定的圆（基圆）作纯滚动时，此动直线上一点的轨迹。

     
对于定传动比的齿轮机构，目前通常采用的齿廓曲线仅有渐开线，摆线及变态摆线等少数几种。

目前绝大部分齿轮都是采用渐开线作为齿廓，称为渐开线齿轮。

什么是渐开线，渐开线画法

将一端系有铅笔的线缠在圆筒的外周上，然后在线绷紧的状态下将线渐渐放开。此时，铅笔所画出的曲线即为渐开曲线。圆筒的外周被称为基圆。

将一个圆轴固定在一个平面上,轴上缠线,拉紧一个线头,让该线绕圆轴运动且始终与圆轴相切,那么线上一个定点在该平面上的轨迹就是渐开线.
直线在圆上纯滚动时,直线上一点K的轨迹称为该圆的渐开线,该圆称为渐开线的基圆,直线称为渐开线的发生线.渐开线的形状仅取决于基圆的大小,基圆越小,渐开线越弯曲；基圆越大,渐开线越平直；基圆为无穷大时,渐开线为斜直线.渐开线方程为：
x=r×cosθ+θ×r×sinθ
y=r×sinθ-θ×r×cosθ
z=0
式中,r为基圆半径；θ为展角,其单位为弧度
展角θ和压力角α之间的关系称为渐开线函数
θ=inv(α)=tan(α)-α
式中,inv为渐开线involute的缩写
渐开线画法:
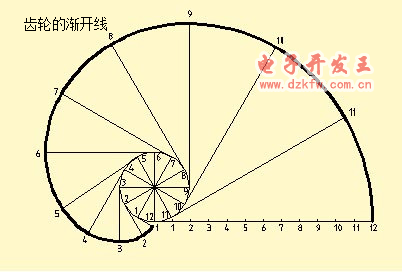
已知圆的直径D,画渐开线的方法如图
(1）将圆周分成若干等分（图中为12等分）,将周长πD作相同等分；
(2）过周长上各等分点作圆的切线；
(3）在第一条切线上,自切点起量取周长的一个等分（πD/12）得点1；在第二条切线上,自切点起量取周长的两个等分（2xπD/12）得点2；依此类推得点3、4、……、12；
(4）用曲线板光滑连接点1、2、3、……、12；即得圆的渐开线.