发电压电晶片工作效应详解

在研究石英晶体的物理性质时发现：当沿着晶片的某些方向施加作用力使晶片发生形变后，晶片上相对的两个表面会出现等量的正、负电荷，电荷面密度与施加的力的大小有关，该现象称为压电现象。具有压电现象的介质为压电体。

在离子性的晶体中，正负离子有规则地交错配置，构成结晶点阵，就形成固有电矩，在晶体表面出现极化电荷，由于晶体暴露在空气中，经过一段时间，这些电荷便被降落到晶面上的空气中的异号离子所中和，因此，极化面电荷和电矩都不会显现。但当晶体发生机械形变时，晶格就会发生变化。这样，电矩产生变化，表面极化电荷数值也发生改变。于是，表面上正电荷或负电荷都有了可以测量的增量，该增量是压电效应电量。

压电效应分为正压电效应和逆压电效应。具体工作原理如图1所示。

 

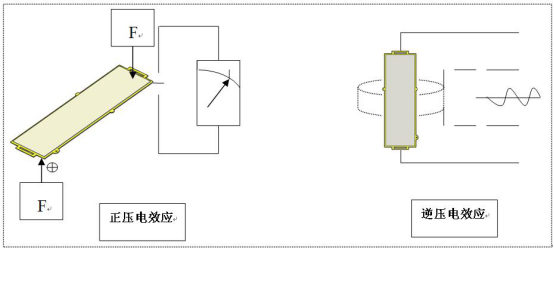
图1 压电效应原理

在无电场作用下，当沿着一定方向对压电体施力而使它产生机械变形时，其内部产生极化现象，相对的两个表面会出现异号电荷，外力与端面积大，出现的电荷就多。端面电荷的符号视外力而定。当外力去掉后，又重新恢复不带电状态的现象，称为正压电效应。当作用力方向改变时，电荷极性也随着改变。若将两个表面装上电极并用导线接通，变化的自由电荷便从一个极板移至另一极板，形成电流。具有压电效应的晶体称为压电晶体。

当在压电体的极化方向施加电场时，压电体就在一定方向上产生机械形变或机械压力，当外电场撤去时，这些形变或压力随之消失的现象称为逆压电效应。逆压电效应的产生，是由于压电晶体受到电场作用时，在晶体内部产生了应力，这种应力称为压电应力，通过它的作用产生压电应变。

因此，压电效应是由于晶体在机械力的作用下发生形变而引起带电粒子的相对位移，从而使晶体的总电矩发生变化而造成的。晶体是否呈现压电性，由构成晶体的原子和离子排列方式决定的。具有对称中心的晶体不可能有压电性。凡是具有正压电效应的晶体，也一定有逆压电效应，具有压电效应的材料称为压电材料。

1.2 压电效应的物理机制

晶体内部正、负离子的偶极矩在外力的作用下由于晶体的形变而被破坏，导致使晶体的电中性被破坏，从而使其在一些特定的方向上的晶体表面出现剩余电电荷而产生的。

压电陶瓷的压电效应机理与压电单晶大不相同，未经极化处理的压电陶瓷材料是不会产生压电效应的。压电陶瓷经极化处理后，剩余极化强度会使与极化方向垂直的两端出现束缚电荷（一端为正，另一端为负），由于这些束缚电荷的作用在陶瓷的两个表面吸附一层来自外界的自由电荷，并使整个压电陶瓷片呈电中性。当对其施加一个与极化方向平行或垂直的外压力，压电陶瓷片将会产生形变，片内束缚电荷层的间距变小，一端的束缚电荷对另一端异号的束缚电荷影响增强，而使表面的自由电荷过剩出现放电现象。当所受到的外力是拉力时，将会出现充电现象。

1.3 压电效应产生的条件

晶体结构没有对称中心。

压电体是电介质。

其结构必须有带正负电荷的质点。即压电体是离子晶体或由离子团组成的分子晶体。

1.4 压电方程

在压电弹性体中，机械效应与电效应是分不开的，它们互相牵制，紧紧耦合在一起。因此，压电方程是压电体的力学量（应力T，应变S）和电学量（电场强度E，电位移D）间的关系方程。表示如下：

式中是在恒定应力（或零应力）下测量出的机械自由介电常数，为电短路情况下测得的弹性常数，为压电常数。第一个方程叙述了正压电效应，第二个方程叙述了逆压电效应。

1.5 压电性能参数

压电发电晶片利用锆钛酸铅（PZT）陶瓷片的正压电效应产生电压和电荷，陶瓷片的压电性能直接影响压电发电晶片的工作性能。其压电性能可由多个压电参数表达，其中与发电晶片相关的参数主要为机电耦合系数，机械品质因数等。现叙述如下：

1、机电耦合系数

机电耦合系数是综合反映压电材料性能的参数。它表示压电材料的机械能与电能的耦合效应，定义为：

或

压电元件的机械能与它的形状和振动方式有关，不同形状和不同振动方式所对应的机电耦合系数不同。

2、机械品质因数

压电体作谐振动时，要克服内部的机械摩擦损耗，再有负载时要克服外部负载的损耗。机械品质因数定义为机械损耗的反比，即：

机械品质因数的存在表明任何压电材料都不能把输入的机械能全部用于输出。机械品质因数越大，能量的损耗就越少。

3、频率常数

压电晶片元件的谐振频率与沿振动方向的长度的乘积为一常数，即频率常数。

  

表示在谐振频率状态下工作具有最好的输出。

4、相对介电常数

相对介电常数反映材料的介电性质或极化性质。定义如下：

2 压电发电鞋理论发电效率分析

压电陶瓷片具有将机械能转化为电能的性能，当其受外力作用时，其极化强度随之而变, 导致表面吸附的自由电荷随之变化。

2.1 等效模型

当一陶瓷片在压力作用下上下表面产生电荷，其相当于一个电容，电容在其两极产生电荷后就储存了一定的能量。从电学角度来看，压电片可以简化为一个正弦电流源，与内在的电极电容 并联，如图2所示。假设电流源和电极电容恒定，负载可调。由戴维南等效定理，该电路中阻抗为：

 

 

 

 

 

 

 

 

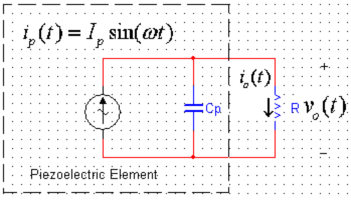
图2 压电片带负载电阻的等效电路

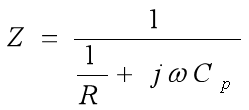即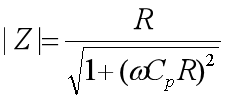     

可求出电路输出电压：

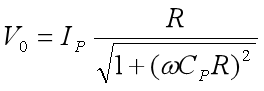
输出功率:

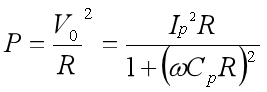
当时，即外接负载电阻和压电片等效阻抗相等时，负载吸收的能量最大。

   

 发电晶片中的陶瓷片工作在厚度伸缩模式下，如图3为压电陶瓷片，其作用面积为A,厚度为h，沿y轴极化，沿y轴方向施加应力F。

 

 

 

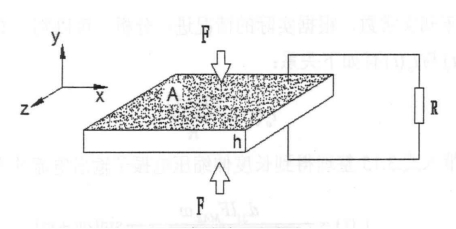
图3 厚度伸缩压电发电振子

 

在外界压力F作用下的压电材料产生的电荷和电压为：

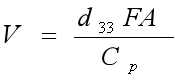
压电片等效为一个电容，其储能的公式是：

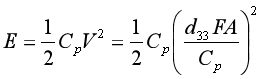
式中： 为压电片的压电常数；F 为作用在压电片表面的应力； 是作用力施加的区域； h分别是压电片的厚度；为压电片的相对介电常数；为真空介电常数。

将上述的公式整理后可得压电片产生的电能为：

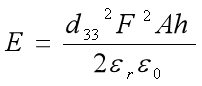
一个人走路时对发电晶片做的功可用以下公式计算：

压电发电晶片的发电效率为;

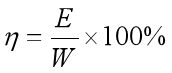
2.2 能量传输和利用效率分析

当作用在压电片上的力消失后，压电元件产生的电荷立即消失。因此，需要外接电容对压电元件产生的电荷进行储存。设压电元件极间电容为，外接电容为C，产生的电能在两者之间再分配，根据传输结束后电压相等的关系，设，其中，C 为外接电容；为压电元件间电容；是设的量，。则电容C 上存储的能量与产生能量的传输效率：

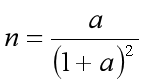
当 ，得到= 1。即时，传输效率最大，此时n = 25%。