利用卡诺图化简逻辑函数的方法称为卡诺图化简法或图形化简法。化简时依据的基本原理就是具有相邻性的最小项可以合并，并消去不同的因子。由于在卡诺图上几何位置相邻与逻辑上的相邻性是一致的，因而从卡诺图上能直观地找出那些具有相邻性的最小项并将其合并化简。

1.合并最小项的规则

(1) 若两个最小项相邻，则可合并为一项并消去一对因子。合并后的结果中只剩下公共因子。

(2)若四个最小项相邻并排列成一个矩形组，则可合并为一项并消去两对因子。合并后的结果中只包含公共因子。

(3)若八个最小项相邻并且排列成一个矩形组，则可合并为一项并消去三对因子。合并后的结果中只包含公共因子。

l 下图给出了最小项相邻的几种情况

最小项相邻的几种情况图

(a)(b) 两个最小项相邻 (c)(d) 四个最小项相邻 (e) 八个最小项相邻

至此，可以归纳出合并最小项的一般规则：如果有 个最小项相邻（n=1，2，…）并排列成一个矩形组，则它们可以合并为一项，并消去n 对因子。合并后的结果中仅包含这些最小项的公共因子。

2. 卡诺图化简法的步骤

用卡诺图化简逻辑函数时可按如下步骤进行：

(1)将函数化为最小项之和的形式。

(2)画出表示该逻辑函数的卡诺图。

(3)找出可以合并的最小项。

(4)选取化简后的乘积项。选取的原则：

n         这些乘积项应包含函数式中所有的最小项（应覆盖卡诺图中所以的1）

n         所用的乘积项数目最少，即可合并的最小项组成的矩形组数目最少

n         每个乘积项包含因子最少，即各可合并的最小项矩形组中应包含尽量多的最小项

例1：用卡诺图化简法将式 化简为最简与—或函数式

解：首先画出表示函数Y的卡诺图，如图  

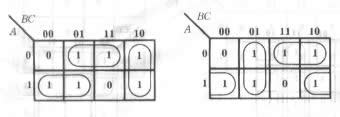
通过合并最小项，得出结果，

左图：

右图：

注：

l         在填写Y的卡诺图时，并不一定要将Y化为最小项之和的形式。

l         需要找出可以何并的最小项，将可能合并的最小项用线圈出，有时存在多种可能合并最小项的方案，所以有时一个逻辑函数的化简结果不是唯一的。

例2：用卡诺图法将 化为最简与—或逻辑式

解：首先画出Y的卡诺图，然后把可能合并的最小项圈出，并按照前面所述的原则选择化简与—或式中的乘积项

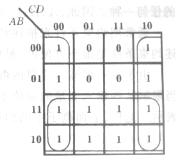
最后得到结果

l         补充说明：在以上的两个例子中，我们都是通过合并卡诺图中的1来求得化简结果的。

但有时也可以通过合并卡诺图中的0先求出 的化简结果，然后再将 求反得到Y。夫妻其原理是因为全部最小项之和为1，所以若将全部最小项之和分成两部分，一部分（卡诺图中填入1的那些最小项）之和记作Y，则根据 可知，其余一部分（卡诺图中填入0的那些最小项）之和必为 。在多变量逻辑函数的卡诺图中，当0的数目远小于1的数目时，采用合并0的方法有时会比合并1来得简单。仍以上例为例，在卡诺图中如果将0合并，则可立即写出 ，则

与合并1得到的化简结果一致。

 此外，在需要将函数化为最简的与或非式时，采用合并0的方式最为适宜，因为得到的结果正是与或非形式。如果要求得到 的化简结果，则采用合并0的方式就更简便了。