化简具有无关项的逻辑函数时，如果能合理利用这些无关项，一般都可得到更加简单的化简结果。

为达到此目的，加入的无关项应与函数式中尽可能多的最小项（包含原有的最小项和已写入的无关项）具有逻辑相邻性。合并最小项时，究竟把卡诺图上的×作为1（即认为函数式中包含了这个最小项）还是作为0（即认为函数式中不包含这个最小项）对待，应以得到的相邻最小项矩形组合最大、而且矩形组合数目最少为原则。

例1：化简逻辑函数

，

给定其约束条件

解：如果不利用约束项，则Y已无可化简。但适当地加进一些约束项以后，可以得到

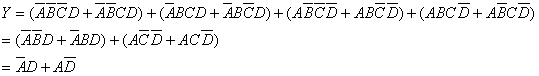
利用了约束项以后，使逻辑函数得以进一步化简。但是代数法表示不够直观。从逻辑函数的卡诺图上则表示得更清晰。

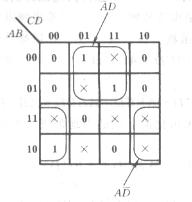
例2： 试化简逻辑函数：

已知其约束条件为：

解：画出函数Y的卡诺图，

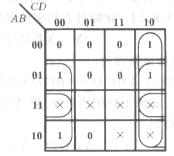
于是得到 ：