这一章我们学习的重点是数字设备进行逻辑运算的基本知识:基本逻辑运算和实现这些运算的门电路。它是本课程的基础,我们要掌握好!
在学习时,我们把它的内容分为:
§ 2、1 基本概念
§ 2、2 三种基本逻辑运算
§ 2、3 常用的复合逻辑
§ 2、4 集成逻辑门
§2、1基本概念
这一节来了解一下逻辑函数、逻辑变量和真值表的概念。
一:逻辑变量与逻辑函数
我们作某些事情,总是先对事情判断一下,然后再根据判断的结论去做。
例如我们吃饭,总是先判断:‘饭做好了吗?’:‘人到齐了吗?’:‘餐桌准备好了吗?’,只有上面的条件都满足了,我们才可以吃饭,否则就不能。
我们把用逻辑语言描述的条件称为逻辑命题,其中的每个逻辑条件我们都称为逻辑变量,我们一般用字母A、B、C、D、、、、、、等表示。把逻辑变量写成函数的形式就称为逻辑函数。
例如:我们把上面我们提到的问题的条件分别用A、B、C表示,那麽它的逻辑函数可表示为:
F=f(A、B、C)
二:真值表
因为逻辑变量只有两种取值0或1,所以我们可以用一种表格来描述逻辑函数的真假关系,我们就称这种表格为真值表。
例如:列出“能吃饭吗?”的真值表。设条件满足为1,不满足为0,我们知一个逻辑变量,有两种组合,三个逻辑变量就有八种组合。所以其真值表为:
| A B C | F |
| 0 0 0 | 0 |
| 0 0 1 | 0 |
| 0 1 0 | 0 |
| 0 1 1 | 0 |
| 1 0 0 | 0 |
| 1 0 1 | 0 |
| 1 1 0 | 0 |
| 1 1 1 | 1 |
§2、2三种基本的逻辑运算
在实际中我们遇到的逻辑问题是多种多样的,其实它们可以用三种基本的逻辑运算把它们概括出来。它们就是‘与’‘或’‘非’逻辑运算。
下面我们用表格来描述一下它们:
| 逻辑运算 | 逻辑表达式 |
逻辑符号 |
二变量运算结果 |
二变量输出波形 |
| 与运算 | F=AB |
0*0=0;0*1=0 |
||
| 或运算 | F=A+B |
0+0=0;0+1=1 |
||
| 非运算 | F=A |
A=0;F=1 |
§2、3 常用的复合逻辑
通过上一节的学习我们已经知道逻辑代数中有三种基本的逻辑运算,事实上我们总是希望用较少的器件来实现较多的功能,所以我们就要用到复合逻辑。
一:常用的复合逻辑
经常用到的复合逻辑有三种:它们是“与非”、“或非”、“与或非”。
| 逻辑名称 | 逻辑表达式 | 逻辑符号 | 逻辑门特性 |
| “与非”逻辑 | F=AB |
输入只要有“0”,输出为“1”,输入全部为“1”输出为“0”。 | |
| “或非”逻辑 | F=A+B |
输入只要有“1”,输出位“0”,输入全部为“0” 输出为“1” | |
| “与或非”逻辑 | F=AB+CD | 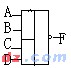 |
我们根据具体情况,来作决定。 |
二:异或”逻辑和“同或”逻辑
有时我们还会用到“异或”逻辑和“同或”逻辑,它们都是两变量的逻辑函数。
“异或”逻辑指输入二变量相异时输出为“1”,相同时输出为“0”。
它的逻辑表达式为:![]() ,逻辑符号为:
,逻辑符号为:![]() 。
。
“同或”逻辑指输入二变量相同时输出位“1”,相异时输出位“0”。
它的逻辑表达式为:![]() ,逻辑符号为:
,逻辑符号为:
。
三:正负逻辑
由于我们的规定不同,逻辑的输入端取值也不相同。我们把输入为正称为正逻辑,输入为负的称为负逻辑。因为我们在逻辑电路中,大多采用硅管,用的是正电源,所以我们一般采用正逻辑。
§2、4 集成逻辑门
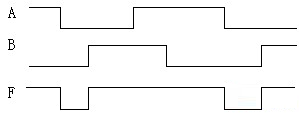
这一节我们来学习由晶体管组成的集成逻辑门的一些基本知识。 例1:如右图所示的三态门,试分析三态门各种输出情况。 由此我们可以看出三态门的输出端的情况与控制端有关,只有控制端为导通时输入端才有效。
集成逻辑门分为两种即双极型集成电路和单极型集成电路。双极型集成电路分为:DTL集成逻辑和TTL集成逻辑;单极型集成电路分为一般MOS逻辑和互补MOS逻辑(CMOS)。
一:双极型集成电路
它的特点是:工作速度高,易于做成大规模集成电路,功耗低等。我们来简单介绍一下双极型集成电路的两种形式(1)TTL集电极开路门(OC门)(2)三态门。
1)TTL集电极开路门(OC门),它的特点是能实现“线与”功能,可以节省门数,减少输出门的级数
它可应用在数据总线上。当每个OC门只要有一个输入端为低电平时,OC门的输出均为高电平。
(2)三态门;它的特点是输出端除了高电平、低电平两种状态外还有第三种状态:高阻状态或禁止状态。
二:单极型集成电路
当E为高电平时 输出端F为高阻状态
当E为低电平是 输出端F=AB
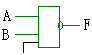
它的特点是:高、低电平都很理想;功耗很低,近似为“0”,任意时刻都有一个关闭;抗干扰能力强;兼容性强
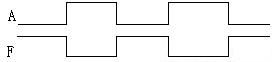
例2:如右图试分析输入控制端的情况。
通过电阻接地时:电阻小于等于700欧姆时相当于输入为:“0”;当电阻大于等于2000欧姆时相当于输入为:“1”

当输入控制端悬空时相当于“1”
接高电平U时相当于“1”
接地时相当于“0”



 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底