上面所得各种变量的卡诺图,其共同特点是可以直接观察相邻项。也就是说,各小方格对应于各变量不同的组合 ,而且上下左右在几何上相邻的方格内只有一个因子有差别,这个重要特点成为卡诺图化简逻辑函数的主要依据。现以4变量卡诺图为例来说明,为清楚起见,把各最小项填入对应方格内,如图1所示。可见,图中各行和各列上下左右相邻的方格内只有一个因子不同,例如,
m4对应于

,
m5对应于

,它们的差别仅在
D和
D,
m5和
m13只差
A和
A,余类推。要特别指出的是,卡诺图水平方向同一行里,最左和最右端的方格也是符合上述相邻规律的,例如,
m4和
m6的差别仅在C和
C。同样,垂直方向同一列里最上端和最下端两个方格也是相邻的,这是因为都只有一个因子有差别。这个特点说明卡诺图呈现循环邻接的特性。
以上各卡诺图变量的排列形式(即卡诺图方格外
A、
B、
C、
D等所表示的变量)是为了获得循环邻接的特性,在满足循环邻接的前提下,卡诺图还有其他形式的画法。
图1所示的卡诺图可以简化成如图2所示。在图2中,用0、1分别表示反变量和原变量,变量
A、
B、
C、
D的每种取值组合,与方格内的最小项一一对应,例如,0000对应于

,1111对应于
ABCD,余类推。这样,只要标出方格外纵、横两向的二元常量,即可由二进制码推出相应的最小项的十进制编号。

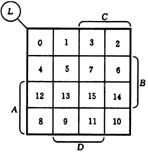
图1 填入最小项的卡诺图 图2 图1的简化<



