解:分析过程如下:
1.写出各逻辑方程式
(1)这是一个同步时序电路,各触发器CP 信号的逻辑表达式可以不写。
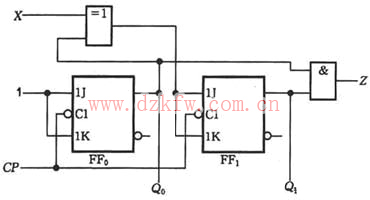
(2)输出方程 Z =Q1nQ0n
(3)驱动方程
J0=1 K0=1
2.将驱动方程代入相应的JK触发器的特征方程,求得各触发器的次态方程为:
|
图1 例1的逻辑电路图 |
3. 列状态表,画状态图和时序图
列状态表是分析时序逻辑电路的关键一步,其具体做法是:先填入电路现态Qn(本例中为Q1n ,Q0n )的所有组合状态以及输入信号X的所有组合状态,然后根据输出方程及状态方程,逐行填入当前输出Z的相应值,以及次态Qn+1(Q1n+1 ,Q0n+1)的相应值。该电路的状态表如表1。根据状态表可作出状态图,如图2所示。
列状态表是分析时序逻辑电路的关键一步,其具体做法是:先填入电路现态Qn(本例中为Q1n ,Q0n )的所有组合状态以及输入信号X的所有组合状态,然后根据输出方程及状态方程,逐行填入当前输出Z的相应值,以及次态Qn+1(Q1n+1 ,Q0n+1)的相应值。该电路的状态表如表1。根据状态表可作出状态图,如图2所示。
|
表1 例1的状态表 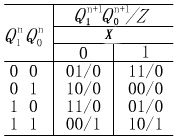 |
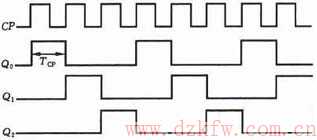
设电路的初始状态为Q1nQ0n=00,根据状态表和状态图,可画出在一系列CP 脉冲作用下电路的时序图,如图3所示。
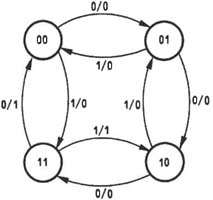 图2 例1的状态图 |
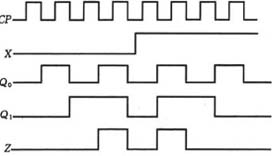 图3 例1电路的时序图 |
4.逻辑功能分析
由该例的状态图就可看出,此电路是一个可控计数器。当X=0时,进行加法计数,在时钟脉冲作用下,Q1Q0的数值从00到11递增,每经过4个时钟脉冲作用后,电路的状态循环一次。同时在Z 端输出一个进位脉冲,因此,Z 是进位信号。当X=1时,进行减1计数,Z 是借位信号。
例2 分析图4所示的逻辑电路
由该例的状态图就可看出,此电路是一个可控计数器。当X=0时,进行加法计数,在时钟脉冲作用下,Q1Q0的数值从00到11递增,每经过4个时钟脉冲作用后,电路的状态循环一次。同时在Z 端输出一个进位脉冲,因此,Z 是进位信号。当X=1时,进行减1计数,Z 是借位信号。
例2 分析图4所示的逻辑电路
|
图4 例2的逻辑电路图 |
解:由图4可见,这是一个同步时序逻辑电路,电路中没有输入信号X,而且电路的输出直接由各触发器的Q 端取出。分析过程如下:
1. 写出各逻辑方程
(1) 输出方程 Z0=QOn Z1=Q1n Z2=Q2n
(2) 驱动方程 D0=Q0nQ1n D1=Q0n D2=Q1n
2. 将驱动方程代入相应的D触发器的特性方程,求得各D 触发器的次态方程
Q0n+1=D0=Q0nQ1n, Q1n+1=D1=Q0n, Q2n+1=D2=Q1n
3. 列状态表,画状态图和时序图
1. 写出各逻辑方程
(1) 输出方程 Z0=QOn Z1=Q1n Z2=Q2n
(2) 驱动方程 D0=Q0nQ1n D1=Q0n D2=Q1n
2. 将驱动方程代入相应的D触发器的特性方程,求得各D 触发器的次态方程
Q0n+1=D0=Q0nQ1n, Q1n+1=D1=Q0n, Q2n+1=D2=Q1n
3. 列状态表,画状态图和时序图
|
表2 例2的状态表 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
 |
|
|
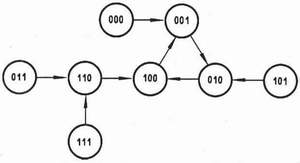
图5 例2的状态图 |
图6 例2的时序图 |
从状态图可见,001,010,100这3个状态形成了闭合回路,在电路正常工作时,电路状态总是按照回路中的箭头方向循环变化,这3个状态构成了有效序列,称它们为有效状态,其余的5个状态称为无效状态(或偏离态)。
4. 逻辑功能分析
该电路的状态表和状态图不太容易直接看出此电路的逻辑功能,而由它的时序图可见,这个电路在正常工作时,各触发器的Q 端轮流出现一个脉冲信号,其宽度为一个CP 周期,即1TCP ,循环周期为3TCP ,这个动作可以看作是在CP 脉冲作用下,电路把宽度为1TCP 的脉冲依次分配给Q0,Q1,Q2各端,所以此电路的功能为脉冲分配器或节拍脉冲产生器。由状态图可知,若此电路由于某种原因进入无效状态时,在CP 脉冲作用后,电路能自动回到有效序列,这种能力称为电路具有自启动能力。



 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底