结 论：用3个节点电压表示了6个支路电压。进一步减少了方程数。

1、节点电压方程

根据KCL，可得图3.2-1电路的节点电压方程

 

节点电压法分析电路的一般步骤
确定参考节点，并给其他独立节点编号。列写节点电压方程，并求解方程，求得各节点电压。由求得的节点电压，再求其他的电路变量，如支路电流、电压等。

例3.2-1 图3.2-1所示电路中，G1=G2=G3=2S，G4=G5=G6=1S， ，，求各支路电流。
解：1. 电路共有4个节点，选取d为参考点，。其他三个独立节点的节点电压分别为。
 

2. 列写节点电压方程
节点a：
节点b：
节点c：
代入参数，并整理，得到

解方程，得

 

3. 求各支路电流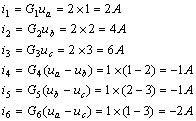

特 别 注 意：节点电压方程的本质是KCL，即Σ(流出电流) =Σ(流入电流)，在节点电压方程中，方程的左边是与节点相连的电导上流出的电流之和，方程的右边则是与节点相连的电流源流入该节点的电流之和。如果某个电流源上还串联有一个电导，那么该电导就不应再计入自电导和互电导之中，因为该电导上的电流（与它串联的电流源的电流）已经计入方程右边了。

例3.2-2 图3.2-2所示电路，试列出它的节点电压方程。

 解：对于节点a，流入的电流源的支路上还串联了一个电阻R1，在计算a点的自电导时，不应再把R1计算进去，所以a点的节点电压方程为

b点的节点电压方程为

2、弥尔曼定理

当电路只有两个节点时，这种电路称为单节偶电路（single node-pair circuit）。对于单节偶电路，有弥尔曼定理。
 

弥尔曼定理：对于只有两个节点的单节偶电路，节偶电压等于流入独立节点的所有电流源电流的代数和除以节偶中所有电导之和。

二、含有电压源的电路
 

1、有伴电压源
结 论：如果电路中的电压源是有伴电压源，将有伴电压源等效成有伴电流源。

方法一 把电压源当电流源处理
把电压源当作电流源看待，并设定电压源的电流，列写节点电压方程。利用“电压源的电压等于其跨接的两个独立节点的节点电压之差”这个关系，再补充一个方程式，联立求解。

2、无伴电压源
 

电压源的一端与参考点相连

结 论
电压源一端与参考点相连，另一端的节点电压就是电压源的电压，节点电压方程减少一个。

方法二 超节点（super node）方法
 

虚线框当作一个超节点处理，列写节点电压方程。
注 意：列写这个超节点的方程时，其中的“自电导×本节点电压”这一项应包括两个部分，即组成该超节点的每个节点的电压与其相应的自电导的乘积。