一. 定义与电路符号
理想变压器也是一种理想的基本电路元件。为了易于理解,我们耦合电感的极限情况来引处它的定义。
图7-6-1(a)是耦合电感的原理结构与磁场分布,图中N1,N2分别为初级与次级线圈的匝数。定义n=N2/N1,n称为变必,也称匝比。
理想变压器的有四个理想化条件:
(1) 无漏磁通,即Φs1=Φs2=0,耦合系数K=1,为全耦合,故有Φ11=Φ21,Φ22=Φ12。
(2) 不消耗能量(即无损失),也不贮存能量。
(3) 初、次级线圈的电感均为无穷大,即L1→∞,L2→∞,但![]() 为有限值。证明如下:
为有限值。证明如下:
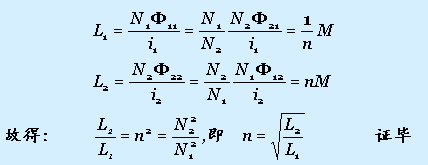
; 
即在全耦合(K=1)时,两线圈的电感之比,是等于其匝数平方之比,亦即每个线圈的电感都是与自己线圈匝数的平方成正比。
(4) 因有K=1,L1→∞,L2→∞,故有![]() →∞。
→∞。
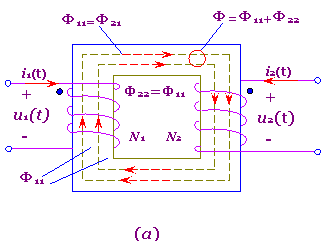


图7-6-1 理想变压器的定义与电路符号
满足以上四个条件的耦合电感称为理想变压器。可见理想变压器可认为是耦合电感的极限情况。即K=1,L1→∞,L2→∞,M→∞的情况,它纯粹是一种变化信号的传输电能的元件,但它与耦合电感在本质上已不同了。耦合电感是依据电磁感应原理工作的,是动态元件,需要三个参数L1,L2,M来描述;而理想变压器已没有了电磁感应的痕迹,是静态元件,只需要一个参数n来描述。理想变压器的电路符号如图7-6-1(b),(c)所示。
理想变压器是电路的基本无源元件之一。工程实际中使用的铁心变压器,在精确度要求不高时,均可用理想变压器作为它的电路模型来进行分析与计算。
二. 伏安方程
从图7-6-1(a)看出,由于无漏磁通,故穿过两个线圈的总磁通相同,均为Φ=Φ21+Φ12=Φ11+Φ22。又由于图中u1(t),i1(t)和Φ三者的参考方向互为关联,u2(t),i2(t)和Φ三者的参考方向也互为关联,故:
u1(t)=N1dΦ/dt
u2(t)=N2dΦ/dt
故有 u1(t)/u2(t)=N1/N2=1/n (7-6-1a)
或 u1(t)=u2(t)/n (7-6-1b)
又因为理想变压器不消耗也不贮存能量,所以它吸收的瞬时功率必为零,即必有
u1(t)i1(t)+u2(t)i1(t)=0
故得 i1(t)/i2(t)=-u2(t)/u1(t)=-N2/N1=-n (7-6-2a)
或 i1(t)=-ni2(t) (7-6-2b)
式(7-6-1),(7-6-2)即为理想变压器的时域伏安方程。可看出:
1. 由于n为大于零的实数,故此两方程均为代数方程。即理想变压器为一静态元件(无记忆元件),已经没有了电磁感应的痕迹,所以能变化直流电压和直流电流。
2. 理想变压器的两线圈的电压与其匝数成正比,两线圈的电流与其匝数成反比,且当n>1时有u2(t)>u1(t),为升压变压器;当n<1时有u2(t)<u1(t),为降压变压器;当n=1是有u2(t)=u1(t),既不升压也不降压。
3. 在电路理论中,我们把能联系两种电路变量 的元件称为相关元件,否则即为非相关性元件。电阻,电感,电容等均为相关性元件,而理想变压器则为非相关性元件,亦即u1(t)与i1(t)之间,u2(t)与i2(t)之间,均无直接的约束关系,它们均各自由外电路决定。
当电路工作在正弦稳态时,式(7-6-1),(7-6-2)即可写为向量形式,即
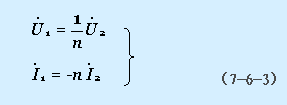
式(7-6-1)和(7-6-2)均是在图7-6-1所示电压参考极性与电流参考方向以及同名端标志下列出的。若线圈的同名端或电压的参考极性,电流的参考方向改变了,则其伏安方程中等号右端的"+","-"号也应相应改变。例如对于图7-6-2(a)、(b)所示电路,则其伏安方程为

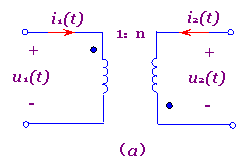
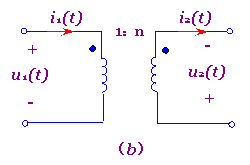
; 图7-6-2 理想变压器电路
(a)同名端改变 (b)i2(t)参考方向和u2(t)参考极性改变
需要指出,从耦合电感的极限来定义理想变压器只是一种方法,是为了使读者易于接受。理想变压器的本质定义应是从数学上来定义,即凡满足式(7-6-1),(7-6-2)伏安方程的电路元件即为理想变压器,其电路符号采用图7-6-1(b),(c)表示,也只是因袭了传统而已,并非一定要由线圈构成。
三. 阻抗变换
设在理想变压器的次级接阻抗Z,如图7-6-3(a)所示,则因有
; 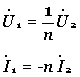
故得原边的输入阻抗为
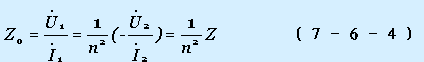

于是可得原边等效电路如图7-6-3(b)所示。从式(7-6-4)看出:
(1) n≠1时,Z0≠Z,这说明理想变压器具有阻抗变换作用。n>1时,Z0>Z; n<1时,Z0<Z。
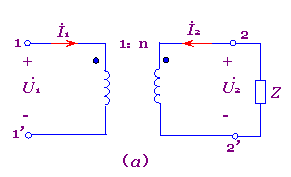
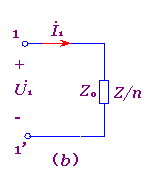
p; 图7-6-3 理想变压器的阻抗变换作用
(2)由于n为大于零的实常数,故Z0与Z的性质全同,即次级的R,L,C,变换到初级相应为R/n2,L/n2,n2C。
(3) 阻抗变换与同名端无关。
(4) 当Z=0时,则Z0=0,即当次级短路时,相当与初级也短路。
(5) Z=∞时,则Z0=∞,即当次级开路时,相当与初级 开路。
(6) 阻抗变换具有可逆性,即也可将原边的阻抗Z变换到副边,如图7-6-4所示。但要注意此时副边的等效阻抗为Z0=n2Z。
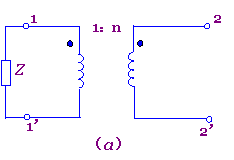

图7-6-4 阻抗变换作用的可逆性
(7) 阻抗在某一边是串联(并联),则变换到另一边也是串联(并联),如图7-6-5所示。

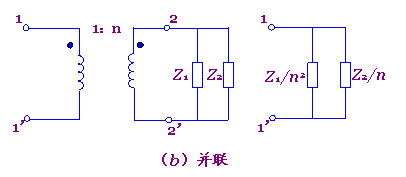
; 图7-6-5 理想变压器阻抗变换作用的性质
由以上的全部叙述可见,理想变压器既能变换电压和电流,也能变换阻抗,因此,人们更确切地称它为变量器。
四. 用受控源模拟理想变压器
将式(7-6-1),(7-6-2)改写为
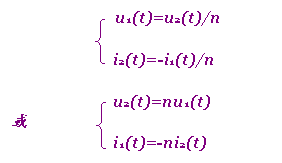
根据此两方程即可将理想变压器用受控源电路来模拟,相应如图7-6-6所示。
这种模拟的意义在于,开辟了实现理想变压器的新途径,使之集成化,微型化成为了可能。例如可用两个回转器级联即可实现;同时也说明了理想变压器也可视为一种点耦合元件,正因为如此,所以它可耦合直流分量,即变换直流电压和直流电流。

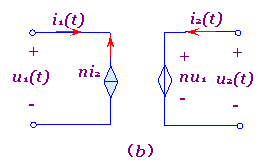
图7-6-6 用受控源模拟理想变压器
五. 含理想变压器电路的分析计算
含理想变压器电路的分析计算,一般仍是应用回路法(网孔法)和节点法等方法,只是在列方程时必须充分考虑它的伏安关系和阻抗变换特性即可解决问题。
例7-6-1 用等效电压源定理求图7-6-7(a)电路中的![]() 。
。

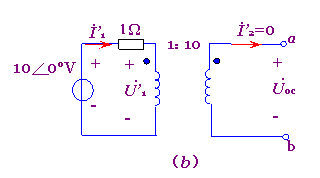
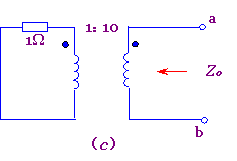
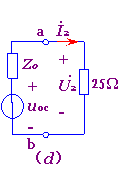
图7-6-7 例7-6-1的电路
解:根据图7-6-7(b)求开路电压 ,从而得![]()
根据图(c)求Z0,即
Z0=102×1=100Ω
其等效电压源电路如图 (d)所示。于是根据图(d)得;
![]()
例7-6-2 图7-6-8电路 ,![]()
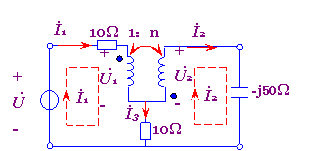
图7-6-8 例7-6-2的电路
解:设理想变压器两边的电压![]() 分别为 则可列出方程:
分别为 则可列出方程:





 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底