机械原理中，根据平面四连杆机构中是否存在曲柄，有一个曲柄或两个曲柄，可把它分为下面三种基本形式。

1，曲柄摇杆机构

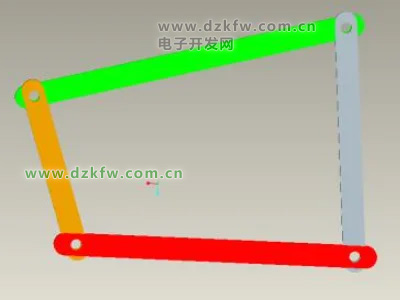
2，双曲柄机构：平面四连杆机构中若有两个曲柄存在，这样的机构称为双曲柄机构。这种机构一般可将主动件的匀速整周转动转换成从动件的非匀速或匀速整周转动。

双曲柄机构中，若两曲柄的长度相等，且连杆与静件的长度也相等，则此机构为平行四边形机构。其运动特点是两曲柄的角速度始终保持相等，连杆在运动过程中始终作平行移动。若改变平行四边形机构，使其两个曲柄转动方向相反，这时的机构称为反向双曲柄机构。

3，双摇杆机构：在平面四连杆机构中，若与静件相联的两杆件均为摇杆，则此机构称为双摇杆机构。

扩展资料：

定理

1，杆长之和条件：平面四杆机构的最短杆和最长杆的长度之和小于或者等于其余两杆长度之和。

2，在铰链四杆机构中，如果某个转动副能够成为周转副，则它所连接的两个构件中，必有一个为最短杆，并且四个构件的长度关系满足杆长之和条件。

3，在有整装副存在的铰链四杆机构中，最短杆两端的转动副均为周转副。此时，如果取最短杆为机架，则得到双曲柄机构；若取最短杆的任何一个相连杆为机架，则得到曲柄摇杆机构；如果取最短杆对面构件为机架，则得到双摇杆机构。

4，如果四杆机构不满足杆长条件，则不论选取哪个构件为机架，所得到机构均为双摇杆机构。

上述系列结论称为格拉霍夫定理。