零状态是零原始状态的简称。电路在零原始状态下,仅由输入激励产生的响应称为零状态响应( zero-state response )。
电路在单位阶跃电压或单位阶跃电流激励下的零状态响应称为单位阶跃响 应 (unit-step response), 简称阶跃响应 (step response) 。
 图1 表示由单位阶跃电流激励的 RC 并联电路。图中ε( t )为单位阶跃电流。当 t<0 时电路无输入激励,
图1 表示由单位阶跃电流激励的 RC 并联电路。图中ε( t )为单位阶跃电流。当 t<0 时电路无输入激励, ![]() ;当 t>0 时,电流源向电路提供1A 的恒定电流。这时,电路中的任一响应( 电流或电压 ) 仅仅是由单位阶跃电流激励产生的,即为电路的 的RC 并联电路
;当 t>0 时,电流源向电路提供1A 的恒定电流。这时,电路中的任一响应( 电流或电压 ) 仅仅是由单位阶跃电流激励产生的,即为电路的 的RC 并联电路
当 t=0 时,由于电容电流是有限值,电容电压不能跳变,故 uc(0 + )= uc(0 - )=0, iR (0 + )=uc(0 +) /R=0 ,ic(0 + )=1A 。即
此时电容的充电电流等于电流源的电流。随着充电过程的进行,电容电压将从零开始逐渐升高,电阻中的电流也将从零开始逐渐增大,但电流源输出的电流 ( 1A )却保持不变,因此,电容电流必将逐步减小。当电容充电结束后, ![]() ,电流源的全部电流通过电阻。
,电流源的全部电流通过电阻。
为了研究上述 RC 并联电路的阶跃响应,首先根据电路的基本约束关系建 立电路方程
![]()
或 ![]() (1 )
(1 )
当 t 〉 0 时,式( 1 )变为
 ( 2 )
( 2 )
此即为 t>0 时电路的输入 - 输出方程,它是一个一阶常系数线性非齐次微分方程。
令式( 2 )的右端等于零,得齐次微分方程 为

于是可得阶跃响应电压的自由分量为 ![]()
由于电路的激励函数在 t>0 时是一个常数,可设阶跃响应电压的强制分量 ![]() 为一常数 K ,即
为一常数 K ,即 ![]() 将此式代入非齐次微分方程式( 2 ),得到
将此式代入非齐次微分方程式( 2 ),得到
![]()
于是有 K=R
强制分量 ![]()
因此式(2 )的通解为 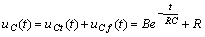 ( 5 )
( 5 )
由式 (5 )令 ![]() ,并代入初始条件
,并代入初始条件 ![]() ,可得
,可得
B+R=0
从而解得积分常数 B=-R
将积分常数代入式( 5 ),并将该式右端乘以单位阶跃函数 ![]() ,便得到电路的阶跃响应电压为
,便得到电路的阶跃响应电压为
![]()
或 ![]()
阶跃响应 ![]() 的强制分量
的强制分量 ![]() 在 t 〉 0 的区间内是一个常量, 因此,
在 t 〉 0 的区间内是一个常量, 因此, ![]() 又被称为阶跃响应
又被称为阶跃响应 ![]() 的稳态分量 (steady-state component) ,或称稳态响应 (steaty-state response) 。线性电路对周期性激励的强迫响应虽不是常量 ( 而是周期量 ) ,也称为稳态响应。
的稳态分量 (steady-state component) ,或称稳态响应 (steaty-state response) 。线性电路对周期性激励的强迫响应虽不是常量 ( 而是周期量 ) ,也称为稳态响应。
阶跃响应 ![]() 的自由分量
的自由分量 ![]() 随时间的增长按指数规律衰减,衰减的 决慢决定于电路的时间常数τ =RC ,当经过 4 τ —5 τ的时间后,即可认为
随时间的增长按指数规律衰减,衰减的 决慢决定于电路的时间常数τ =RC ,当经过 4 τ —5 τ的时间后,即可认为 ![]() 已消失。因此,阶跃响应
已消失。因此,阶跃响应 ![]() 的自由分量又被称为暂态分量 (transient component) ,或称暂态响应 ( transient response) 。当暂态分量衰减完后,阶跃响应即等于其稳态分量。显然,这就是电路中的电容在充电结束后(
的自由分量又被称为暂态分量 (transient component) ,或称暂态响应 ( transient response) 。当暂态分量衰减完后,阶跃响应即等于其稳态分量。显然,这就是电路中的电容在充电结束后( ![]() ) 具有的电压。
) 具有的电压。
但须注意,暂态响应不一定等于自然响应,稳态响应不一定等于强迫响应。 如果激励函数是随时间的增长而衰减的 ( 例如指数脉冲 ) ,则受激励函数约束的强迫响应也将随时间的增长而衰减,它与激励同时存在,同时消逝。这时稳态响应等于零,自然响应和强迫响应一并组成暂态响应。
在暂态响应存在的时间内,电路的工作状态称为暂态 ( 或瞬变状态 ) 。暂态响应衰减完以后,电路的工作状态称为稳定状态 ( 简称稳态 ) 。图1 所示电路在经过 4 τ -5 τ的时间后、即可认为进入稳定状态,此时电路的响应即为稳态响应。
电阻电流和电容电流可根据欧姆定律和基尔霍夫电流定律分别表示为
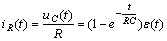
![]()
阶跃响应 ![]() 、
、 ![]() 、
、 ![]() 的函数曲线分别描绘在图2 中。由此 可见,
的函数曲线分别描绘在图2 中。由此 可见, ![]() 与
与 ![]() 都是从它们的初始值开始,随时间的增长按指数规律单调地上升,而
都是从它们的初始值开始,随时间的增长按指数规律单调地上升,而 ![]() 则是从它的初始值开始随时间的增长按同一指数规律衰减,约经 4 τ —5 τ的时间后,它们分别等于各自的稳态分量 ( 电容电流的稳态分量为零 ) 。但电容电流在 t=0 时,由
则是从它的初始值开始随时间的增长按同一指数规律衰减,约经 4 τ —5 τ的时间后,它们分别等于各自的稳态分量 ( 电容电流的稳态分量为零 ) 。但电容电流在 t=0 时,由 ![]() 跳变到
跳变到 ![]() 。
。
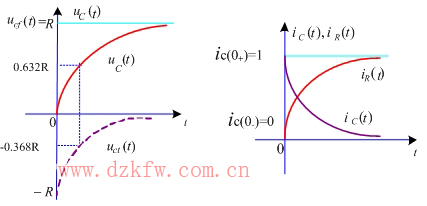
(a)电容电压及其稳态分量与暂态分量 (b)电流曲线
图2 RC并联电路的阶跃响应曲线
根据以上所得结果,不难看出,一阶电路对阶跃激励的零状态响应是激励的线性函数。事实上,零状态响应是电路在零原始状态下仅由输人激励产生的响应,因而自然是激励的线性函数。这对于线性电路而官,具有普遍意义。
上面讨论了一阶电路的阶跃响应。如果作用于同一电路的激励函数是移位的单位阶跃函数 ![]() ,则因电路参数不随时间变化,电路的输山响应与输入激励施加于电路的时刻无关,响应函数的曲线应与阶跃响应曲线完全相同,仅仅在时间上延迟
,则因电路参数不随时间变化,电路的输山响应与输入激励施加于电路的时刻无关,响应函数的曲线应与阶跃响应曲线完全相同,仅仅在时间上延迟 ![]() ;这就是所谓电路的非时变性。例如图1 所示 RC 并联电路的阶跃响应电压 [ 式〔 6)] 为
;这就是所谓电路的非时变性。例如图1 所示 RC 并联电路的阶跃响应电压 [ 式〔 6)] 为 ![]()
激励函数 ![]() 与响应
与响应 ![]() 的曲线示于图 6(a) 与图 6(b) 中。根据以上分析可得移位的单位阶跃电流激励
的曲线示于图 6(a) 与图 6(b) 中。根据以上分析可得移位的单位阶跃电流激励 ![]() 作用于同一电路的零状态
作用于同一电路的零状态
响应电压为
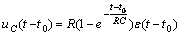
![]() 与
与 ![]() 的曲线示于图 6(c) 与图 6(d) 中。
的曲线示于图 6(c) 与图 6(d) 中。
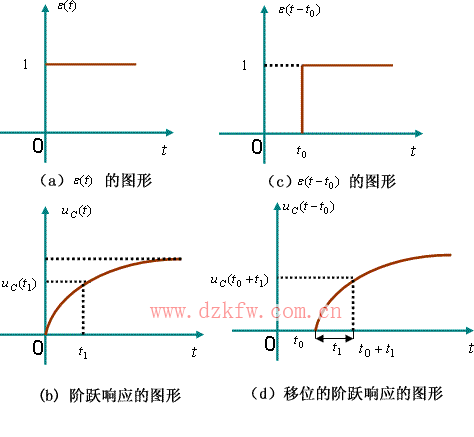
图6 电路的非时变性的应用示例


 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底