LC正弦波振荡电路分为变压器反馈式振荡器和电感三点式振荡器以及电容三点式振荡器三种电路形式。
　　
　　1、首先分析变压器反馈式振荡器的振荡条件。
　　
　　1)相位平衡条件的判断：
　　
　　判断相位平街条件是否满足的方法，仍用瞬时极性法。即判断电路的反馈是否是正极性的。具体说就是断开回路，引进输入，看反馈信号与输入信号是否同相，若为同相，则是正反镇，相位平街条件满足，否则就不满足。
　　
　　具体步骤是：如图(a)所示，其反馈元件为L1，由它给放大电路提供反馈电压。设断开A、B两点，在A点处加入一个瞬时极性为“+”的信号，如果我们能确定该信号经过放大、反馈回到B点时还是“+”的，那么电路中的反馈就是正极性的。

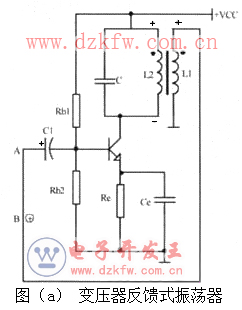
　　具体过程：当A点为“+”时，三极管的集电极为“-”(共发放大电路输出与输入相位相反)，即L2的无点端是“-”，则有点端是“+”，根据瞬时极性法中同名端极性相同的原则，则L1的有点端也是“+”，即B点是“+”，所以电路是正反馈，电路满足相位条件。
　　
　　若将L1的有点端和无点端调换一下，如图(b)所示，则电路引进的是负反馈，不满足相位平衡条件，电路不能振荡。

　　
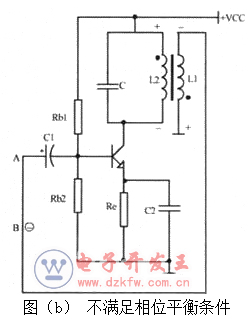
　　2)振幅平衡条件的判断：
　　
　　判断振幅平衡条件就是要判断电路是否满足AF=1。从理论上讲，对于一个已知电路和元件参数的振荡电路来说，应该能够通过计算的方法或测量的方法求得A和F的值，然后求二者的乘积即能完成判断，然而实际中不可能采用这种方法。
　　
　　实际所用方法的步骤是：检查放大电路的结构，分析其是否具有合适的静态工作点，如果电路有合适的偏置，就认为放大电路可以提供所需的放大倍数A。然后检查反馈电路的结构，如果能找到反馈电压Vf，即反馈电路能够提供反馈电压，那么就可以认为反馈电路能提供振荡电路所需的反馈系数F，以上两步完成了，振荡电路就满足振幅平衡条件。
　　
　　在图(a)中，Rb1和Rb2是两个上、下偏置电阻，Re是发射极电阻，只要它们的阻值大小合适，电路就能获得合适的静态工作点。其反馈元件为L1，由它给放大电路提供正反馈电压，可得知，电路满足振幅平衡条件。
　　
　　由上可知，图(a)的变压器反馈式振荡器能同时满足振幅平衡条件和相位平衡条件，所以电路能够振荡。
　　
　　如果将图中的Cb短路后，电路还能振荡吗？若将Cb短路，如图(c)所示，则L1将基极电位短路，即VBE：0，三极管因发射结零偏而处于截止状态，所以无论怎样调整它的偏置元件，也不可能使三极管获得合适的静态工作点，所以图(C)电路不满足振幅平街条件而不能振荡。

　　2、分析电感三点式振荡器和电容三点式振荡器的振荡条件。
　　
　　1）振幅平街条件的判断：
　　
　　与变压器反馈式振荡器的判断方法相同。
　　
　　2)相位平街条件的判断：
　　
　　不论是电感三点式振荡器还是电容三点式振荡器，相位平街条件的判断一般不直接采用瞬时极性法，而是使用一种由瞬时极性法演变而得到的更为简单的方法，其具体内容是：接在三极管发射极与集电极，发射极与基极之间的电抗必须为同性质电抗(同为电感或同为电容），接在集电极和基极之间的电抗必须为异性质电抗(若前者为电容，后者应为电感；若前者为电感，则后者应为电容)，电路才满足相位条件。
　　
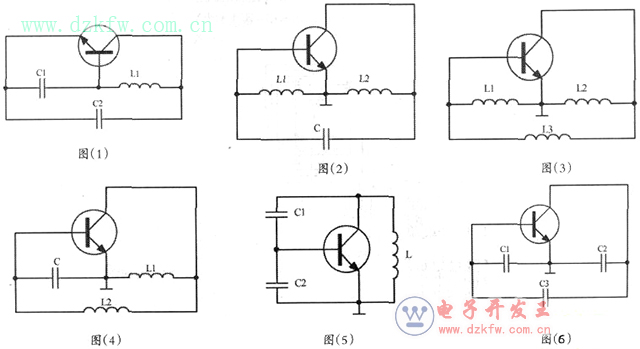
　　现举例说明：在下图所示的三点式交流通路中，哪些电路满足相位平衡条件？
　　
　　图(1)中接在三极管发射极与集电极，发射极与基极之间同为电容，而接在集电极和基极之间的元件为电感，故满足相位平衡条件。且正反馈元件为C1。
　　
　　图{2)中接在三极管发射极与集电极，发射极与基极之间同为电感，而接在集电极和基极之间的元件为电容，故满足相位平衡条件。且正反馈元件为L1。
　　
　　图(3)、图(4)、图(5)、图(6)均不满足三点式振荡器的相位平衡条件的要求，所以都不能振荡。
　　
　　需要强调的是，三点式振荡器中正反馈元件的查找。那么怎样才能正确找到这些正反馈元件呢？
　　
　　其实很简单，在三点式振荡器中，只要在LC选频网络中找到在交流通路中一端接地、另一端接输入端的元件，这个元件就是使电路满足相位平衡条件的正反馈元件。比如在图(1)中，这是一个共基极的振荡电路，其输入端是发射极而不是集电极(集电极是不能作为输入端的)，C1是接在发射极与地之间，也就是说是接在输入端与地之间，所以是C1正反馈元件，而C2却是一端接地，另一端接输出端，所以它不是正反馈元件。在图(2)中，电路是共发射极的振荡电路，基极是输入端，L1接在基极与地之间，也就是接在输入端与地之间，敌正反馈元件是L1而不是L2。