会员中心
会员注册1、数学表达式
有介质存在时，高斯定理仍然成立。但在计算高斯面内包围的电荷时，应包括自由电荷
和极化电荷
，即
而
两式整理后，得
如果定义一点的电位移矢量
为
则有
上式称为有介质存在时的高斯定理。因为
是电位移矢量的通量，所以它可以表述为：通过任一闭合曲面的电位移通量，等于包围在该闭合面内自由电荷的代数和。
2、关于定理的几点说明
（1）有介质存在时的高斯定理是更普遍的规律，它概括了真空中的高斯定理。
（2）在
的高斯定理中，
和
不直接出现，在电荷和介质分布具有一定对称性的情况下，可以由自由电荷
的分布，求出
的分布。
（3）高斯面上任一点的
是由空间总的自由电荷的分布决定，不能认为只与面内自由电荷有关。
1、物理意义
是复合量，它既描述电场，同时也描述介质极化。引进
的目的是为了使有介质存在时高斯定理的形式简化。2、
与
的关系 因为
，所以
而 
，所以
三、应用举例
半径为
的金属球，电荷为
，放在均匀无限大介质中，介质的介电常数为
。 求介质中的电场强度。
|
解：在金属球外的介质中取一点
电位移矢量 |
 |
，
距球心的距离为
。以
为球心、
为半径作一同心球面为高斯面，则由介质中的高斯定理，得
介质中的场强为
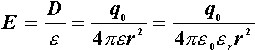
若金属球放在真空中，则场强为
返回顶部
刷新页面
下到页底