电通量:在讲述静电场的高斯定理之前,我们将借助于电场线的概念,引入电通量这个物理量。在电场中任一点处,取一块面积元![]() ,与该点场强
,与该点场强![]() 的方向相垂直,我们把场强大小
的方向相垂直,我们把场强大小![]() 与面积元
与面积元![]() 之乘积,称为穿过该面积元的电通量,用
之乘积,称为穿过该面积元的电通量,用![]() 表示,即
表示,即

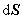 。于是上式可表示为常用的矢量形式,即
。于是上式可表示为常用的矢量形式,即Tags:电通量,电磁学
责任编辑:admin相关文章列表
磁化强度和磁化电流什么是静电感应
导体的静电平衡条件
电场线的方向和特点
磁场的高斯定理
磁路及其基本定律
磁路和磁路定律
电磁波的波动方程
磁路和磁性物质的磁性能
什么是磁场
什么是磁场 磁感强度
电磁感应定律_法拉第电磁感应定律_楞次定律_右手定则
什么是无线输电技术?
高斯定理的应用
磁场对载流导线的作用
洛伦兹力
电磁骚扰传播或耦合机理
静电屏蔽、静磁屏蔽和高频电磁场屏蔽
热电现象,温差电效应:塞贝克效应、帕尔贴效应、汤姆逊效应
带电粒子在静电场中的偏转
电势差
电势能
【实验方法】测量磁感应强度的方法有哪些_测量磁感应强度九种方法
电缆截面积越大,每平方载流量越小,真的和集肤效应有关吗
什么是集肤效应_电流的集肤效应
图文详解 电磁学发展史
安培环路定律
磁感应线(磁力线)
磁感应强度叠加原理,毕—萨定律
安培力的功
[ 查看全部 ] 网友评论
推荐文章
最新推荐
热门文章


 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底