在加性高斯白噪声（AWGN）信道中，可以使用匹配滤波器实现数字信号的最佳接收。匹配滤波器是一种最佳线性滤波器，它是在输出信噪比最大准则下设计的一个线性滤波器，准确地说，匹配滤波器使其输出信噪比在某一特定时刻上达到最大值。
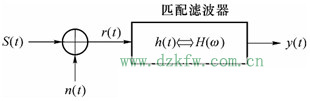
　　匹配滤波器具有特别重要的意义。例如在二进制数字传输中，我们关心的是能够从噪声中正确地判断两种可能信号中出现哪一种，判断时刻的信噪比愈高，愈有益于作出正确的判决。
　　一、匹配滤波器原理
　　设匹配滤波器的传输函数为，冲激响应为，并将匹配滤波器输入输出分别记为和，如图1所示。图中匹配滤波器输入为 　　式中，为匹配滤波器的输入信号，噪声是零均值高斯白噪声，其双边功率谱密度为。 图1 匹配滤波器原理框图 　　根据线性系统的叠加原理，匹配滤波器的输出为 　　其中，输出信号的表达式为 　　式中，是输入信号的频谱函数。
　　输出噪声的平均功率为 　　则匹配滤波器在时刻的输出信号瞬时功率与噪声平均功率之比为 　　为了寻找一个以使最大，可将许瓦兹不等式用于上式的分子，有 　　显见，当为 　　不等式（6）为等式，此时有最大可能输出信噪比为 　　式中，是信号的能量。
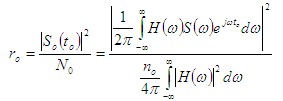
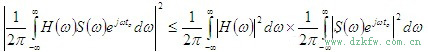
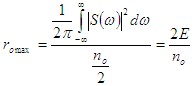
　　由此我们得出结论：在白噪声干扰的背景下，按设计的线性滤波器，将能在给定时刻上获得最大的输出信噪比。由于该线性滤波器的传输特性与输入信号频谱的复共轭相一致，故称其为匹配滤波器。
　　求式的傅里叶反变换，得匹配滤波器的单位冲激响应为 　　可见，匹配滤波器的冲激响应便是信号的镜像信号在时间上平移。
　　作为数字信号的接收滤波器，匹配滤波器应该是物理可实现的。对于线性系统，物理可实现的条件是：当时，有。
　　为了满足物理可实现条件要求： 　　即 　　上式表明，物理可实现的匹配滤波器，其输入信号必须在它输出最大信噪比的出现时刻之前消失（等于零）。也就是说，若输入在时刻瞬间消失，则只有时匹配滤波器才是物理可实现的。一般地，总是希望尽量小些，故通常选择。
　　匹配滤波器的输出信号波形 　　上式表明，匹配滤波器的输出信号波形是输入信号波形的自相关函数的k倍。
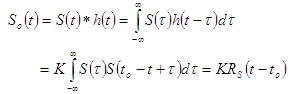
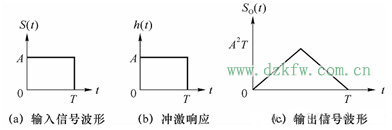
　　例1 设匹配滤波器的输入信号是一单个脉冲，如图2（a）所示，试求匹配滤波器的特性和输出信号波形。 图2 匹配滤波器的输入输出波形及特性 　　解：令K=1，并取，则匹配滤波器的冲激响应为 　　求的傅里叶变换，得匹配滤波器的传输函数为 　　若将看作是理想积分器的传输函数，为延迟电路的传输函数，那么，由上式可得到一种与单个输入脉冲相匹配的匹配滤波器的实现方法，如图3所示。 图3 单个矩形脉冲的匹配滤波器 　　输出信号波形为 　　输出信号波形在时达到最大值。及分别如图7.3.2（b）和（c）所示。
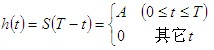
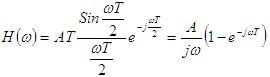
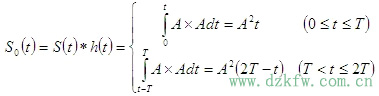
　　二、二进制确知信号的匹配滤波接收
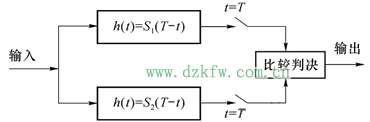
　　二进制数字信号中的两个不同波形和。在抽样时刻对抽样值进行比较判决，哪个匹配滤波器的输出抽样值大，就判决哪个为输出。
　　匹配滤波器构成的接收机方框图如图4所示。图中，有两个匹配滤波器， 图4 利用匹配滤波器的最佳接收机方框图