一、磁感应强度矢量B

1、磁场的外在表现：

（1）对电流有作用力。

（2）对磁铁有作用力。

（3）对运动电荷有作用力。

 2、磁场对运动电荷作用力的特征

（1）有零力线方向：在磁场中总有一个特殊方向，当电荷在磁场中沿该方向运动时不受力，该方向称为零力线方向，该方向与运动电荷无关，反映了磁场本身的性质，规定该方向为磁感应强度矢量B的方向。

（2）运动电荷受到的磁场作用力总是与零力线方向和速度方向垂直。

（3）当v与零力线方向有夹角α时，在任一点受力F∝qvsinα，当v与零力线方向垂直时受力最大，即F_┴∝qv_┴ 。

(4) 当q和v_┴改变时，F_┴的大小也改变，但比值F_┴/（q v_┴）在任一点总是常量，显然，该比值反映了磁场在该点的性质，与运动试探电荷无关，我们可利用该比值来定义描述场本身特性的物理量    磁感应强度矢量B 。

3、磁感应强度矢量B的定义

在第一章中，问题的分析过程是：电荷间

有力的作用，引入电场，用试探电荷测量

电场，定义电场强度E，求出点电荷的场

强公式，引入场强叠加原理，根据点电荷的场强公式和场强叠加原理求场强分布（场强叠加法）。在本章中，也要引入场的概念，后给出产生场的规律。

磁场中某点的磁感应强度是一个矢量，其大小等于单位试探电荷以单位速率垂直零力线方向运动时在该点所受力的大小，其方向满足v×B指向F的方向。其数学表示式为B=F/qV

单位：特斯拉（T），1T=1×10⁴G高斯

二、磁感应线（磁力线）

磁感应线：形象描述磁感应强度空间分布的曲线；实际上并不存在。

规定：

（1）磁感应线上任一点的切线方向等于该点磁感应强度矢量B的方向；

（2）垂直穿过单位面积的磁感应线的根数等于该点磁感应强度的大小。

三、毕奥—萨伐尔斯定律

毕奥   萨伐尔定律主要描述电流元产生的磁场的大小及方向的一个基本定律，它与电场中的点电荷的场强公式相对应，是一个实验定律，但无法用实验直接验证。

在19 世纪20年代，毕奥和萨伐尔对电流产生的磁场分布作了许多实验研究，并和拉普拉斯一起研究和分析了很多实验资料，得到了对应微元段电流产生的磁感应强度计算公式。

1、电流元

设在真空中有电流强度为I的任意形状的载流导线，其导线截面与所考察的场点P的距离比较可略去不计，这样的电流称为线电流。在线电流上取长为dl的定向线元dl，规定dl的方向与线元内的电流密度j的方向相同，并将乘积Idl称为电流元。

2、毕奥   萨伐尔定律

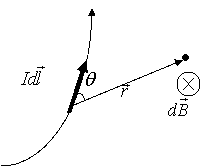
电流元Idl在任一场点P产生的磁场的磁感应强度dB的大小与电流元的大小Idl成正比，与电流元到P点的距离r的平方成反比，还与Idl同r之间夹角的正弦sinθ成正比。

分析表明，dB的方向总垂直于dl与r所构成的平面，并沿dl×r的方向（见图），故可用矢量式表述为：

上式称为毕奥—萨伐尔定律。

由毕奥—萨伐尔定律可知，电流元Idl产生的

dB所对应的磁感应线，是以Idl所在的延长线

为轴，以rsinθ为半径的圆。在同一圆周上各点的dB相等，并随r增大而减小，但位于轴线上各点的dB却等于零。