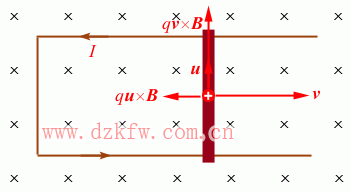
一导体棒在平行导轨上滑动，并与导轨形成回路，匀强磁场B垂直与回路平面。现以恒定外力向右拉动导体棒，棒上产生动生电动势，在回路中出现感应电流。感应电流在磁场中又受到向左的安培力，阻碍导体棒向右运动。当安培力增大到与外力相平衡时，导体棒开始以匀速v运动。此时回路中的感应电流也达到稳定值，载流子在导体棒中将以稳定的漂移速度u相对于导体棒作定向运动。

    因此在平衡时，导体棒中的载流子参与两个运动：随导体棒以速度v平动和沿导体棒以速度u漂移。

    设载流子电量为q，则载流子受到洛仑兹力

洛仑兹力对载流子的功率为

上式右边第一项是产生动生电动势的非静电力的功率，因u与qv×B同方向，此项大于零，故非静电力做正功；第二项是宏观上表现为安培力的分力的功率，因v与qu×B反方向，此项小于零，故安培力做负功。

    由矢量混合积公式可知

    将上式应用到(16.2.5) 式，可得洛仑兹力对载流子的功率为零，这表明非静电力做的正功和安培力做的负功两者大小相等，正好抵消。

    洛仑兹力对载流子（运动电荷）不做功，即洛仑兹力并不提供能量，只是传递能量。在这里，外力克服洛仑兹力的一个分量qu×B所做的功，通过另一个分量qv×B转换为感应电流的能量。这实质上表示能量的转换和守恒。

    根据以上分析，我们发现动生电动势产生过程中的能量转换关系：

    外力做正功输入机械能，安培力做负功吸收了它，同时感应电流以电能的形式在回路中输出这份能量。

    发电机的工作原理就是靠洛仑兹力将机械能转换为电能。