运算放大器是一种多端电子器件,最早开始应用于1940年,首先应用于模拟计算机上,作为基本运算单元,可以完成加减、积分和微分、乘除等数学运算。自1960年后,随着半导体集成工艺的发展,运算放大器逐步集成化,大大降低了成本,其应用远远超出了模拟计算机的界限,在信号运算、信号处理、信号测量及波形产生等方面获得广泛应用。
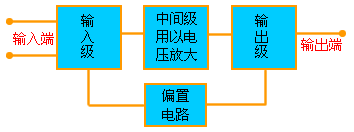
集成运算放大器的电路如图1所示,可分为输入级、中间级、输出级和偏置电路四个基本组成部分。
 |
|
图1 |
2. 运算放大器的电路符号
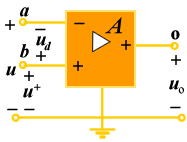
应用运算放大器时感兴趣的是它的外部特性及管脚的用途,图2为F007(5G24)运算放大器的符号图,图中的‘三角形'符号表示放大器,其主要管脚的用途是:2号为反相输入端;3 号为同相输入端;4和7号为电源端;6号为输出端;1和5号端子为外接调零电位器。
 |
 |
|
图 2 |
图 3 |
a端:反向输入端。由此端输入电压u-,则输出信号和输入信号是反向的。
b端:同向输入端。由此端输入电压u+,则输出信号和输入信号是同向的。
o端:输出端 , 输出电压uo
图中A 表示开环电压放大倍数,可达十几万倍。
需要注意的是:不要把图中a端和b端的“-”号和“+”号误认为电压参考方向的正负极性,如图所示,电压参考方要另外标出,均为对地的电压,当在接地端未画出时尤须注意。
3. 运算放大器的静特性
在运算放大器的输入端a 加电压u-, 输入端b 加电压u+,如图3所示,可得输出uo和输入电压的关系:

uo和ud之间的传输特性曲线如图4所示,也称为运算放大器的外特性。其传输特性可分三个区域:
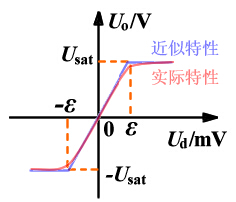
| ①线性工作区: 此时  则 则 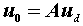 ②正向饱和区: 此时  则 则 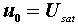 ③反向饱和区: 此时 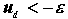 则 则 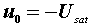 式中e是一个数值很小的电压,例如Usat=13V, A =105 时,则e =0.13mV 。 | |
4.运算放大器的电路模型
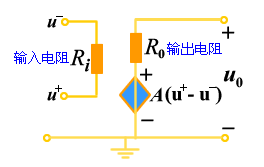
图5给出了运算放大器的电路模型,其输入电阻Ri远大于输出电阻Ro ,输出电压u 0近似为受控电压源的电压,即:
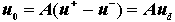 当同向输入端接地:
当同向输入端接地:u+=0, 则 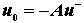 当反向输入端接地:
当反向输入端接地: 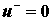 , 则 , 则  |
 |
|
图 5 运算放大器的电路模型 |
5.理想运算放大器
在线性放大区分析运算放大器时,一般可将它看成是一个理想运算放大器,把运放电路作如下的理想化处理:
1) 放大倍数 A→∞
若输出电压uo为有限值,则当放大倍数A→∞ 时,必须满足ud=0 ,即输入电压u+=u-,两个输入端之间相当于短路(虚短路);
2) 输入电阻Ri→∞
若输入电阻Ri→∞ ,则认为输入端电流i+=0,i-=0 。即从输入端看进去,元件相当于开路 (虚断路)。
3) 输出电阻R0→0
由于实际运算放大器的上述指标接近理想化的条件,因此在分析使用理想运算放大器代替实际运算放大器所引起的误差并不严重,在工程上是允许的,但这样却使分析过程大为简化。


 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底