磁感应线是套连载闭合载流回路上的闭合线。若取磁感应强线的环路积分,则因B与dL的夹角θ=0,cosθ=1,故在每条线上![]() ,从而
,从而![]() 。安培环路定理就是反映磁感应这一特点的。
。安培环路定理就是反映磁感应这一特点的。
安培环路定理:磁感应强度沿任何闭合环路L的线积分,等于穿过这环路所有电流强度的代数和的μ0倍。用公式表示有:![]() 。
。
其中电流I的正负规定如下:当穿过回路L的电流方向与回路L的环绕方向服从右手法则时,I>0,反之,I<0。如果电流不穿过回路L,则它对上式右端无贡献。

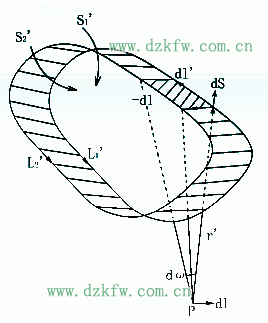
其中![]() 代表dS对场点P所张的立体角dω,沿L'的积分代表整个载流回路作位移-dl时扫过的带状面对P点所张的立体角ω。所以
代表dS对场点P所张的立体角dω,沿L'的积分代表整个载流回路作位移-dl时扫过的带状面对P点所张的立体角ω。所以![]() 。
。
假设以L'为边界作一曲面S',S'对P点也张有一定的立体角Ω。当L'平移时,Ω随之改变。如上图L2'和L1'分别是L'沿-dl平移前后的新、旧位置,令S2'和S1'代表S'的相应位置,Ω2和Ω1代表相应的立体角。因S2'和S1'和带状面组成闭合曲面,它对于外边的P点所张的总立体角Ω2-Ω1+ω=0,所以:
![]()
由于dl是任意的,从而![]() ,即磁场正比于载流线圈对场点所张立体角的梯度。
,即磁场正比于载流线圈对场点所张立体角的梯度。
假设场点P沿闭合的安培环路L移动一周,则环路积分 将正比于立体角Ω在此过程中的总改变量ΔΩ。如果L不与L'套连,则ΔΩ=0,于是:![]() 但是,当L与L'套连时,ΔΩ=4π。因此:
但是,当L与L'套连时,ΔΩ=4π。因此:![]() 。所以安培环路定理得证。
。所以安培环路定理得证。
注意:该定理表达式中各物理量的意义。I只包括穿过闭合回路L的电流。B代表空间所有电流产生的磁场强度的矢量和,其中也包括那些不穿过L的电流产生的磁场,只不过后者的磁场沿闭合环路积分后的总效果为0。I只包括穿过闭合回路L的电流。


 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底