世界上第一台计算机

认真读了之前一篇科普文章的读者会问：“为什么计算机的CPU主要由逻辑门组成？”恭喜你，这说明你不仅“学”而且“思”了。逻辑门可以搭建逻辑电路，完成推理和判断。但计算机更重要的能力还是计算。如果逻辑门不能完成计算，其作用就有限了。那么逻辑门能完成计算吗？

从三角函数到微积分的所有计算，归根到底都可以分解为“加、减、乘、除”计算，而它们又可以归结为“加法”计算。因为减法等于加上负数，乘法等于多次加法，除法等于多次减法。因此，只要逻辑门可以构成“加法器”，理论上就可以完成所有计算。

逻辑门构成加法器的关键，就是大名鼎鼎的二进制。早在1679年，伟大的数学家莱布尼兹就发明了二进制。就凭这一项发明，莱布尼兹对科学的贡献度就应该不在牛顿之下。

我们日常熟悉的十进制有九个符号：0、1、2、3、4、5、6、7、8、9，逢10进1。二进制只有两个符号：0、1，逢2进1。图1是二进制与十进制对照表。

图1 二进制

从图中可以看出，只要记住逢2进1，二进制的加法计算与我们熟悉的十进制是相同的，而且更加简洁。采用一些简单的数学技巧，二进制数与十进制数可以相互换算。

图2是4位二进制数的加法运算：

图2 二进制加法运算

从图2可以分解出二进制加法的2个环节：

相加不进位

相加进位

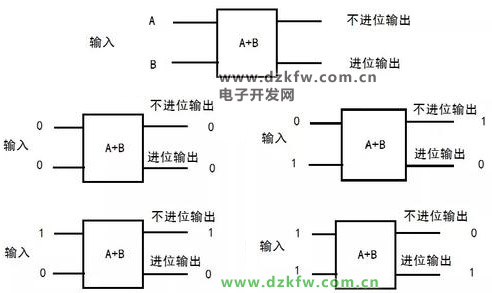
图3 二进制相加分解

图中右下角就是记0进1的意思。

从图3可以看出，进位与不进位输出正好是2种逻辑门，如图4所示：

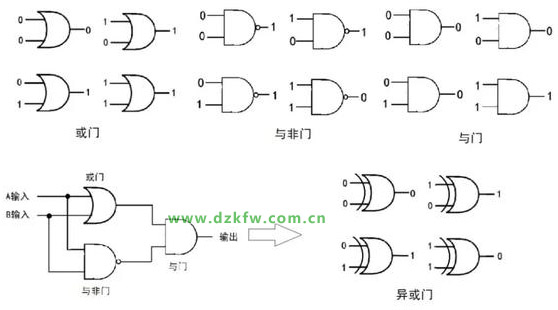
图4 与二进制等价的2种逻辑门

图中的进位输出恰好就是与（AND）门。而不进位输出可以用图5的被称为“异或门”的逻辑门构成：

图5 不进位输出逻辑门：异或门

用或门、与非门、与门构成图5左下角的逻辑电路，称为异或（XOR）门。有兴趣的读者不妨用A=0 ，A=1，B=0，B=1输入逻辑门，仔细运算验证，其输入输出关系恰好就是二进制加法的不进位输出。

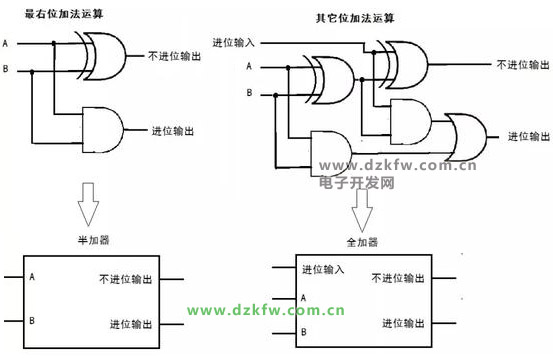
现在我们可以用逻辑门来完成图二进制加法，如图6。

图6 半加器、全加器

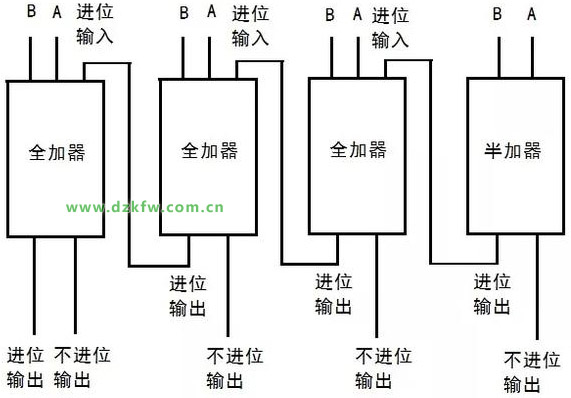
任意多少位的二进制加法器都可以用图6所示的半加器、全加器构成，如图7。

图7 用半加器、全加器构成的加法器

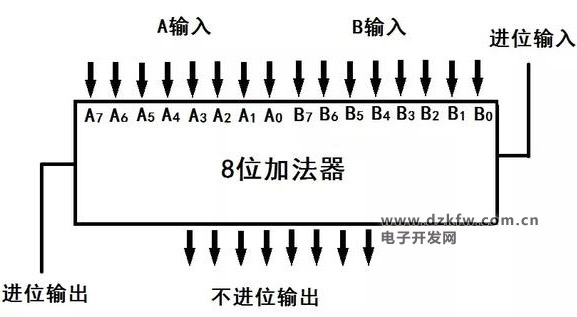
图7是加法器的原理示意图，将其输入输出重新排列，就可以得到通常的加法器原理图，如图8所示。

图8 8位加法器原理图

用2个8位加法器串联就可以构成16位加法器。至此，我们就清楚了逻辑门构成加法器的原理，从而也就理解了逻辑门完成计算的基本原理。但是请读者们务必注意，以上的描述只是逻辑门完成计算的基本原理，实际过程要复杂许多。