什么是方波、矩形波、修正正弦波、纯正弦波?如图所示：

 
　　一、方波：

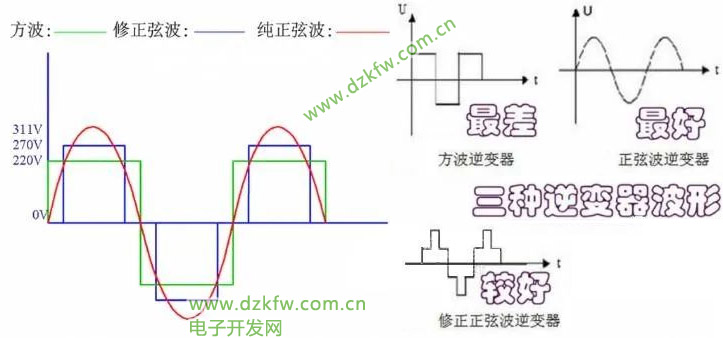
　　方波是一种周期性的波形信号，其电压在两个不同的电平之间交替。方波的特点是在正负电压值之间瞬间切换，没有平滑过渡。换句话说，方波的上升和下降边缘非常陡峭，几乎是垂直的。方波的形状比正弦波和三角波等其他波形更简单。

　　方波具有下列特征：

　　时间占空比：方波的时间占空比是指在一个周期内，电压处于高状态的时间占总周期时间的比率。一个理想的方波有一个50%的占空比，即高和低倍相等。

　　奇次谐波：方波的频谱特征表明，方波只含有奇次谐波，且其幅值随频率的增加而逐渐减小。这就意味着方波中含有大量的高频成分，会引起电磁干扰和信号失真等问题。

　　无偶次谐波：对应于奇次谐波，方波不包含偶次谐波。这是因为方波关于时间轴是对称的，而偶次谐波关于时间轴是反对称的，所以它们对方波的贡献为零。

　　方波广泛应用于数字电路、定时器、逻辑控制、开关电源等领域。然而，对于需要连续、平滑交流电源的应用(如驱动电机或为敏感电子设备供电)，方波不适合，因为其高频成分会导致额外的损耗和干扰。这种情况下，正弦波或者其他更接近正弦波的东西会是更好的选择。

 
方波与矩形波
　　二、矩形波：

　　矩形波是一种常见的信号波形，广泛应用于电子工程、通信工程、计算机科学等领域。

　　矩形波也是一种周期性的波形，其特点是在一个周期内，波形会在一个电平上保持一段时间，然后在另一个电平上保持一段时间，这种波形可用于PWM(脉冲宽度调制)控制、音频信号合成等。在PWM控制中，矩形波可以通过改变占空比来控制输出电压的大小，从而实现对电机、灯等设备的控制。在音频信号合成中，矩形波可以通过添加滤波器来处理，以产生各种音色。

　　三、修正正弦波：

　　修正波是在波形上经过调整或校正的波形。在电力电子领域，最常见的修改波形是修正正弦波，它是在方波的基础上进行改进，使之更接近于纯正弦波。修正正弦波在形状上介于方波和纯正弦波之间。

　　修正正弦波通常由一个短暂的零电压相位和随后的两个不同电压电平的相位组成。在一个周期内，修正后的正弦波在高电平、零电平和低电平之间交替。方波相比，修正正弦波含有更少的高频成分，更接近纯正弦波的特性，从而减少信号失真和电磁干扰。

　　与纯正弦波相比，修正正弦波具有成本低、结构简单的优点。但改造后的正弦波输出的交流波形仍存在一定程度的失真，可能会对一些敏感的电子设备造成影响。对于波形要求较高的应用，纯正弦波通常是更合适的选择。

　　四、纯正弦波：

　　纯正弦波是一种平滑、连续、周期性的波形，其电压随时间按正弦函数变化。纯正弦波具有以下特点：

　　波形平滑：与方波、修正正弦波相比，纯正弦波波形平滑、连续，无突变、无锐边。这使得纯正弦波更适合于对波形敏感的应用，如驱动电动机和音频设备。

　　单一频率：纯正弦波只包含一个基频，没有高阶谐波。这意味着纯正弦波不会产生电磁干扰和信号失真等问题，可以提供更稳定、更清洁的电力。

　　对称性：纯正弦波具有关于时间轴的对称性，即在一个周期内，正半周期和负半周期的波形完全相同。这有助于减少设备上的机械和电气应力。

　　纯正弦波输出的交流电波形更接近理想交流电，更适合对波形要求更高的应用场景。然而，纯正弦波的制造成本和复杂性通常是高的。

五、方波怎样变成正弦波？
方波转成正弦波的方法有很多介绍几种方法给你：

1. 利用D/A转换芯片，把数字信号转成模拟信号。

2. 利用函数发生芯片，把方波转成正弦波

3. 利用文氏电桥振荡电路，把方波转成正弦波

方波转正弦波有方波的傅立叶展开有（傅立叶变换能将满足一定条件的某个函数表示成三角函数（正弦和或余弦函数）或者它们的积分的线性组合），就是说方波可以拆成正弦波的形式，经过一定计算可以将方波拆分成，一次，三次，五次，

截至频率f=1/(2πRC)，所以如果方波频率是100Hz,RC=0.00159, 方波频率是1000Hz，RC=0.000159，只要根据现场情况决定电容电阻的大小就行（乘积一定）一般用多几个电容电阻效果更好，也就是多阶滤波.