(1)平均功率
设对称三相电路中一相负载吸收的功率等于 Pp=UpIpcosφ, 其中Up、Ip 为负载上的相电压和相电流。则 三相总功率为:
P =3Pp =3UpIpcosφ
注意:
1) 上式中的 φ 为相电压与相电流的相位差角 ( 阻抗角 ) ;
2) cosφ为每相的功率因数,在对称三相制中三相功率因数:
cosφA=cosφB=cosφC= cosφ;
3) 公式计算的是电源发出的功率 ( 或负载吸收的功率 ) 。
当负载为星形连接时,负载端的线电压
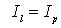 ,代入上式中有:
,代入上式中有: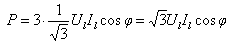
当负载为三角形连接时,负载端的线电压
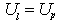 ,线电流
,线电流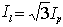 ,代入上式中有:
,代入上式中有: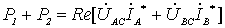
(2) 无功功率
对称三相电路中负载吸收的无功功率等于各相 无功功率之和:
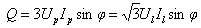
(3) 视在功率
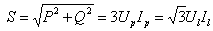
(4)对称三相负载的瞬时功率
设对称三相负载 A 相的电压电流为:
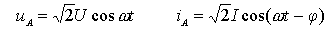
则各相的瞬时功率分别为:
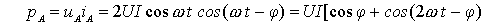
可以证明它们的和为: 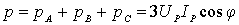
上式表明,对称三相电路的瞬时功率是一个常量,其值等于平均功率,这是对称三相电路的优点之一,反映在三相电动机上,就得到均衡的电磁力矩,避免了机械振动,这是单相电动机所不具有的。
2. 三相功率的测量
(1) 三表法
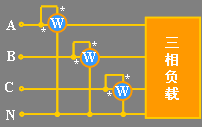
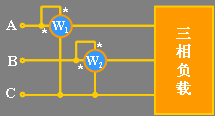
对三相四线制电路,可以用图11.15 所示的三个功率表测量平均频率。若负载对称,则只需一个表,读数乘以 3 即可。
上式表明,对称三相电路的瞬时功率是一个常量,其值等于平均功率,这是对称三相电路的优点之一,反映在三相电动机上,就得到均衡的电磁力矩,避免了机械振动,这是单相电动机所不具有的。
2. 三相功率的测量
(1) 三表法
对三相四线制电路,可以用图11.15 所示的三个功率表测量平均频率。若负载对称,则只需一个表,读数乘以 3 即可。
 |
 |
|
图 11.15 |
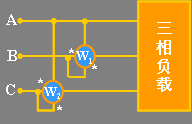
图 11.16 |
(2) 二表法
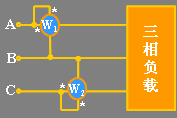
对三相三线制电路,可以用图 11.16 所示的两个功率表测量平均频率。测量线路的接法是将两个功率表的电流线圈串到任意两相中,电压线圈的同名端接到其电流线圈所串的线上,电压线圈的非同名端接到另一相没有串功率表的线上。显然除了图 11.16 的接线方式,还可采用图 11.17 的接线方式。这种方法称为两瓦计法。
对三相三线制电路,可以用图 11.16 所示的两个功率表测量平均频率。测量线路的接法是将两个功率表的电流线圈串到任意两相中,电压线圈的同名端接到其电流线圈所串的线上,电压线圈的非同名端接到另一相没有串功率表的线上。显然除了图 11.16 的接线方式,还可采用图 11.17 的接线方式。这种方法称为两瓦计法。
 |
 |
|
图 11.17 |
两瓦计法中若 W1 的读数为 P1 , W2 的读数为 P2 ,可以证明三相总功率为:
P = P1 + P2
证明: 设负载是 Y 连接,根据功率表的工作原理,有:
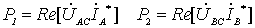
所以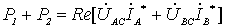
因为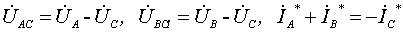 代入上式有:
代入上式有:
P = P1 + P2
证明: 设负载是 Y 连接,根据功率表的工作原理,有:
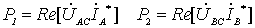
所以
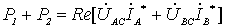
因为
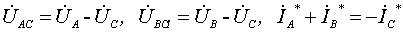 代入上式有:
代入上式有: 所以两个功率表的读数的代数和就是三相总功率。由于△联接负载可以变为 Y 型联接,故结论仍成立。
注意:
1) 只有在三相三线制条件下,才能用二瓦计法,且不论负载对称与否;
2) 两块表读数的代数和为三相总功率,每块表单独的读数无意义;
3) 按正确极性接线时,二表中可能有一个表的读数为负,此时功率表指针反转,将其电流线圈极性反接后,指针指向正数,但此时读数应记为负值;
4) 负载对称情况下,有:
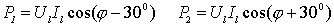
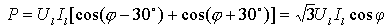
下表给出了不同 φ 值时两个功率表的取值。
注意:
1) 只有在三相三线制条件下,才能用二瓦计法,且不论负载对称与否;
2) 两块表读数的代数和为三相总功率,每块表单独的读数无意义;
3) 按正确极性接线时,二表中可能有一个表的读数为负,此时功率表指针反转,将其电流线圈极性反接后,指针指向正数,但此时读数应记为负值;
4) 负载对称情况下,有:
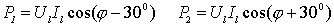
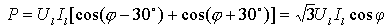
下表给出了不同 φ 值时两个功率表的取值。


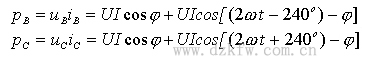
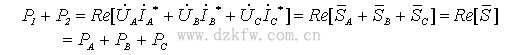

 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底