| 一、毕奥-萨伐尔定律 |
| 1.毕奥-萨伐尔定律:载流导线产生磁场的基本规律。微分形式为: 整个闭合回路产生的磁场是各电流元所产生的元磁场dB的叠加。 |
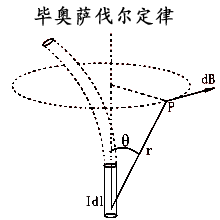 |
| 磁感应线的方向服从右手定则,如图。 |
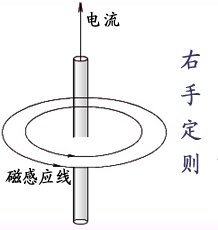 |
| 二、毕奥-萨伐尔定律应用举例 |
| 两种基本电流周围的磁感应强度的分布:载流直导线;圆电流。 例1.载流长直导线的磁场 |
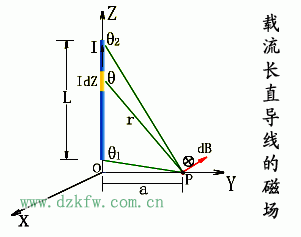 |
解:建立如图坐标系,在载流直导线上,任取一电流元Idz,由毕-萨定律得元电流在P点产生的磁感应强度大小为: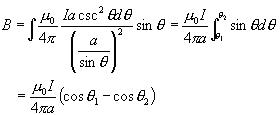 讨论:(1)无限长直通电导线的磁场: (2)半无限长直通电导线的磁场: (3)其他例子 |
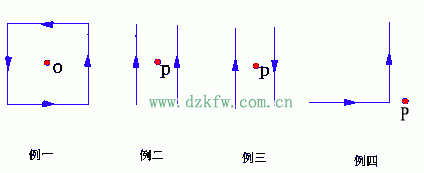 |
| 例2:圆形载流导线轴线上的磁场:设在真空中,有一半径为 R ,通电流为 I 的细导线圆环,求其轴线上距圆心 O 为 x 处的P点的磁感应强度。 解:建立坐标系如图, |
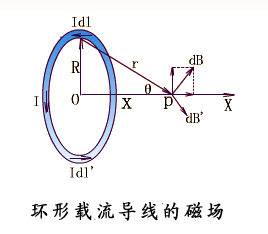 |
任取电流元 ,由毕-萨定律得: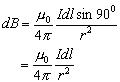 ,方向如图: ,方向如图:将dB进行正交分解: 所以有: 所以: 所以: 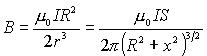  ,方向:沿x轴正方向,与电流成右螺旋关系。 ,方向:沿x轴正方向,与电流成右螺旋关系。讨论:(1)圆心处的磁场:x=0 , (2)当 即P点远离圆环电流时,P点的磁感应强度为: 例3:设有一密绕直螺线管。半径为 R ,通电流 I。总长度L,总匝数N(单位长度绕有n 匝线圈),试求管内部轴线上一点 P 处的磁感应强度。 |
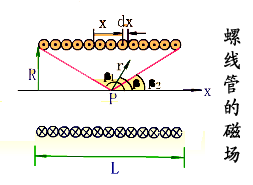 |
解:建立坐标系,在距P 点 x 处任意截取一小段 dx ,其线圈匝数为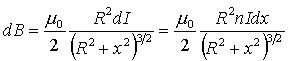 。 。因为螺线管各小段在P点的磁感应强度的方向均沿轴线向右,所以整个螺线管在P点的磁感应强度的大小为: 因为: 代入上式得: 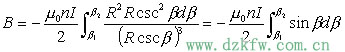 所以: 讨论: (1)管内轴线上中点的磁场: 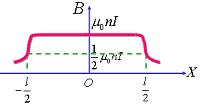 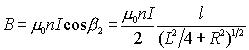 (2)当 L>>R时,为无限长螺线管。此时, (3)半无限长螺线管左端面(或右端面),此时: 因此: |


 返回顶部
返回顶部 刷新页面
刷新页面 下到页底
下到页底