什么是波长？

波长（wavelength）是指波在一个振动周期内传播的距离。也就是沿着波的传播方向，相邻两个振动位相相差2π的点之间的距离。波长λ等于波速u和周期T的乘积，即λ=uT。同一频率的波在不同介质中以不同速度传播，所以波长也不同。波长（或可换算成频率）是波的一个重要特征指标，是波的性质的量度。例如：声波可以从它的频率来量度，人耳可听的声波从20Hz到20kHz，相应的波长从17m到17mm不等；人眼的可见光从深红色的760nm波长，到紫色的390nm波长。

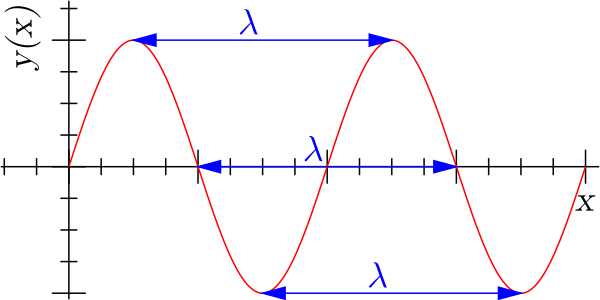
可见光的波长是多少？

可见光是电磁波谱中人眼可以感知的部分，可见光谱没有精确的范围；一般人的眼睛可以感知的电磁波的波长在400～760nm之间，但还有一些人能够感知到波长大约在380～780nm之间的电磁波。正常视力的人眼对波长约为555nm的电磁波最为敏感，这种电磁波处于光学频谱的绿光区域。人眼可以看见的光的范围受大气层影响。大气层对于大部分的电磁辐射来讲都是不透明的，只有可见光波段和其他少数如无线电通讯波段等例外。不少其他生物能看见的光波范围跟人类不一样，例如包括蜜蜂在内的一些昆虫能看见紫外线波段，对于寻找花蜜有很大帮助。最近的一项研究发现，可见光也有可能“透视”肉身。

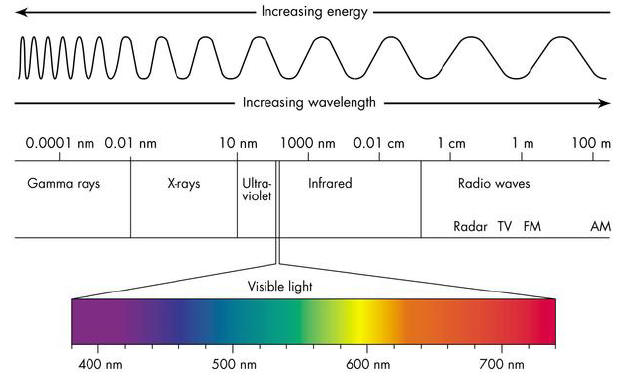
什么是主波长？

任何一个颜色都可以看作为用某一个光谱色按一定比例与一个参照光源（如CIE标准光源A、B、C等，等能光源E，标准照明体D65等）相混合而匹配出来的颜色，这个光谱色就是颜色的主波长。光谱色：就是CIE色度图中外围的一圈轨迹线上的光色。在这条轨迹线上，所有的光都是纯色光。主波长是用来描述观察非纯色光的颜色所对应的某个纯色光波长的颜色。也就是说，不同色光的主波长可能对应于同一个波长值。也可反过来说，具有相同主波长值的两种光，可能具有不同的光色。用“主波长”来表示光，可以理解为，该光不是纯色光。颜色的主波长相当于人眼观测到的颜色的色调（心理量）。若已获得被测LED器件的色度坐标，就可以采用等能白光E光源（x0=0.333314，y0=0.333288）作为参照光源来计算决定颜色的主波长。计算时根据色度图上连接参照光源色度点与样品颜色色度点的直线的斜率，查表读出直线与光谱轨迹的交点，确定主波长。

波长与频率是什么关系？

频率，是单位时间内完成周期性变化的次数，是描述周期运动频繁程度的量，常用符号f或u表示，单位为秒分之一。
波长（wave length）是指波在一个振动周期内传播的距离。也就是沿着波的传播方向，相邻两个振动位相相差2π的点之间的距离。波长λ等于波速V和周期T的乘积，即λ=VT。

横波与纵波的又是什么？

波长指沿着波的传播方向，在波的图形中两个相对平衡位置之间的位移。横波与纵波的波长所代表的意义是不同的。在横波中，波长是指相邻两个相位相差   的点的距离，通常是相邻的波锋、波谷或对应的过零点。在纵波中，波长是指相邻两个密部或疏部之间的距离。波长在物理中常表示为λ，国际单位是米（m）。

波长公式？

高中物理题目涉及到的波长公式有三个，分别如下：

（1）λ=uT   公式中，u为波速，T为振动周期，λ为波长。

（2）λ=u/f  公式中，u为波速，f为振动频率，λ为波长。

（3）Lλ=d△x

这是利用双缝干涉实验来测量光波波长的波长公式。公式中，L为双缝到光屏的距离，λ为波长，d为双缝距离，△x为相邻的两个干涉明纹间的距离。这是高中物理教材选修3-4光的本性中的内容。此外，还经常通过读图来确定波长的大小。通过读图确定波长大小的方法：两个相邻的波峰（或波谷）在x轴上的距离，即为波长λ的大小。具体见下方光的波长测量的解释。

波长的读音？

波长拼音：bō cháng，
波长的符号怎么读？ λ lambda lambd 兰布达

波长单位um怎么读？： 微米

 波长的单位就是长度的单位，标准是m（米）。但一般波长多是在电磁波/光的特性表征中使用，而电磁波/光波的波长大都非常短（频率高），基本上是以毫米（mm)/微米(μm)的单位长表示。所以可以可以读毫米或微米。还有一种仅在表示光波长的单位，称为唉（Å，=10纳米）

波长的英文读音：wavelength 英 [ˈweɪvleŋθ] 美 [ˈwevˌlɛŋkθ, -ˌlɛŋθ]

波长的英文介绍：

In physics, the wavelength is the spatial period of a periodic wave—the distance over which the wave's shape repeats.[1][2] It is thus the inverse of the spatial frequency. Wavelength is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings and is a characteristic of both traveling waves and standing waves, as well as other spatial wave patterns.[3][4] Wavelength is commonly designated by the Greek letter lambda (λ). The term wavelength is also sometimes applied to modulated waves, and to the sinusoidal envelopes of modulated waves or waves formed by interference of several sinusoids.

Assuming a sinusoidal wave moving at a fixed wave speed, wavelength is inversely proportional to frequency of the wave: waves with higher frequencies have shorter wavelengths, and lower frequencies have longer wavelengths.

Wavelength depends on the medium (for example, vacuum, air, or water) that a wave travels through. Examples of wave-like phenomena are sound waves, light, water waves and periodic electrical signals in a conductor. A sound wave is a variation in air pressure, while in light and other electromagnetic radiation the strength of the electric and the magnetic field vary. Water waves are variations in the height of a body of water. In a crystal lattice vibration, atomic positions vary.

Wavelength is a measure of the distance between repetitions of a shape feature such as peaks, valleys, or zero-crossings, not a measure of how far any given particle moves. For example, in sinusoidal waves over deep water a particle near the water's surface moves in a circle of the same diameter as the wave height, unrelated to wavelength.[7] The range of wavelengths or frequencies for wave phenomena is called a spectrum. The name originated with the visible light spectrum but now can be applied to the entire electromagnetic spectrum as well as to a sound spectrum or vibration spectrum.