导读：1.一维流动的质量守恒；2.连续方程的一般形式；3.连续方程的分析与应用。

一维流动的质量守恒

首先来看一下一维流动中的质量守恒，质量守恒决定了，在流动中任意流体微团的质量都应该保持不变。数学表达式是这样的： 其中质量与密度和体积的乘积来表示。因为在流体力学中，通常用来表示速度，这里用B来表示体积。很显然，这种表达式是拉格朗日方法，是针对一个流体微团的。 

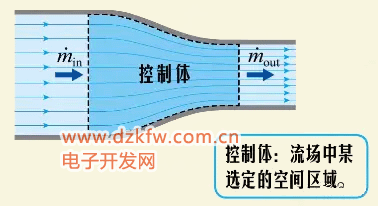
现在来看看流体力学的欧拉法中的质量守恒。在这样一个一维流动中，取中间一段作为控制体流体，从左边流入右边流出。

 

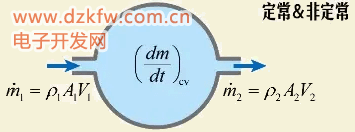
根据质量守恒可知，控制体内质量的增加等于流入的质量减去流出的质量 这就是质量守恒在欧拉法中的表现形式。 当流动为定常时，控制体内的质量保持不变，于是可知，任意时刻流入控制体的质量等于流出控制体的质量： 

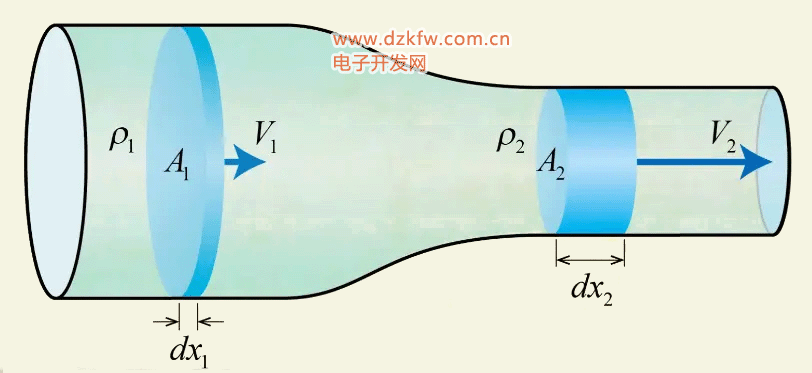
这里的m表示了单位时间流过的质量，称为流量。我们通过这样一个图来看看流量与流速的关系。 

 

对于定常流动单位时间流过进口和出口截面的质量相等，质量等于密度与体积的乘积。在直径大和直径小的地方，同样体积的流体所占流向长度是不同的，这个流向长度与时间的比值就是当地的流速。于是我们就得出了流量的表达式：通过横截面的质量流量等于密度、横截面积和流速三者的乘积，而体积流量等于横截面积和流速的乘积。 

质量守恒在流体力学中体现为流量连续，所以称为连续方程：  当流动为不可压缩时，密度不变，连续方程可以表示为：   

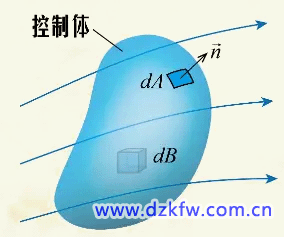
连续方程的一般形式

现在来看看连续方程的一般形式。既三维复杂流动中的质量守恒，在流场中取这样一个任意的控制体，其表面称为控制面:

 

根据质量守恒，单位时间控制体内质量的减少，应该等于流出控制体的质量。于是我们可以写出连续方程的积分形式的表达式：

 

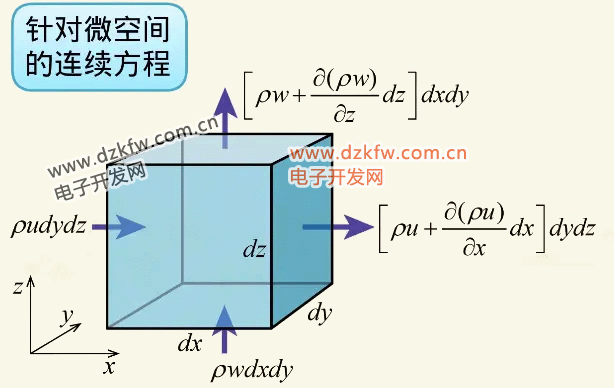
这种积分形式适用于做理论分析，如果要具体计算流场参数需要用到微分形式，所以我们现在来针对微小的控制体推导连续方程。取这样一个六面体为控制体。

 

在六个面上流体可以流入和流出在左侧面和下侧面上进入的流量表达式为 而右侧面和上侧面上流量的表达式用相应的一阶泰勒展开表示： 由于控制体体积不变，控制体内单位时间质量减少就体现为密度的减少： 而根据图中所示，左右两个侧面上的流量之差是净流出的质量： 于是，我们可以得到所有六个面上的净流出量： 质量的减少等于净流出量，于是就可以得出我们所需要的关系是： 体积项  可以消去，就得到连续方程的表达式： 这个表达式是分量形式的，可以简化写成矢量形式： 其中的  是拉普拉斯算子，而  称为密流，即单位面积的流量。

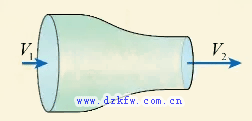
连续方程的分析与应用

现在我们来分析一下连续方程在具体应用时的特点。首先，这个方程的第一项表示了控制体内密度的变化，当流动为定常时，这一项应该为零。于是我们得到定常流动的连续方程，即密流的散度为零： 进一步可以得到一维定常流动的连续方程:当流动维不可压时，得到一维定常不可压流动的连续方程： 也就是说，一维定常不可压流动中流速沿流向保持不变。可是这个推导是不是有问题呢？很显然。对于因为收缩通道内的流速沿流向是增加的。

 

这个推导是看不出问题的。其实，问题在于收缩通道的流动不是一维流动。在工程上把它当作一维流动处理，把另外两位的速度变化用面积变化来表现了。

从连续方程还可以进行这样的变换，把对密度和速度的微分展开成两项： 可以看出。这个式前两项是密度的随体导数，而连续方程可以写成这样： 因为全导数表示的是流体微团密度的变化，所以这是拉格朗日法的连续方程。这种形式的联系方程的物理意义也是很明确的，流体微团的质量变化可以认为有密度和体积两种因素，这个连续方程里面的第一项表示了密度的变化，第二项表示了体积的变化。由于流体微团质量保持不变，所以密度增加，体积必然减小，反之亦然。

从拉格朗日法的连续方程还可以得出，不可压缩流动的连续方程，就是速度的散度为零： 物理意义是流体微团的体积变化为零。

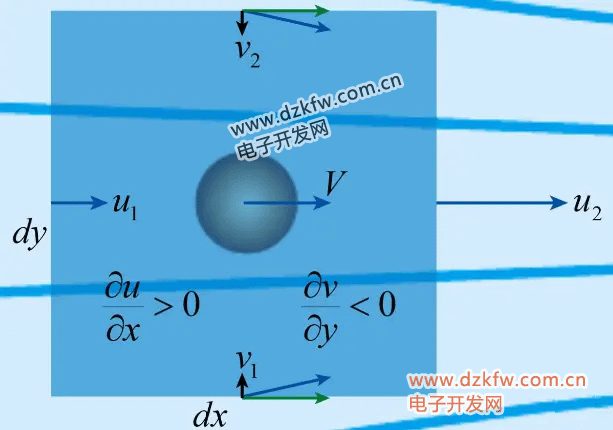
我们再来看一下，所谓因为收缩通道的流动，这次加上不可压的条件来分析收缩通道中部一点处的速度变化情况。

 

在这一点的邻域取一个微小的控制体，其上下左右各面的速度如图所示。左右侧面只有x方向的速度，右侧面的速度比左侧面大，上下表面速度的x分量相同，y分量大小相等方向相反。于是可知u沿x方向是增加的，而v沿y方向是减小的。

 

把二维不可压连续方程写出来： 可以看出和流场分析是一致的，这两项的符号必然相反，而且大小应该相等。从这里我们可以看出x方向速度的增加，伴随着y方向速度的减小，所以收缩流动至少是二维的，而不可能是一维的。

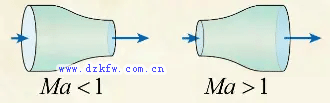
现在来看看压缩性的影响，当流动为可压缩时，连续方程中的密度会改变，低速流动中的密度的变化相对较小，因此收缩就加速在定性上总是正确的。当气体以超音速流动时，密度的变化很大，比速度的变化量还要大，也就是说这时速度增加一倍，密度会减小的比一半还小，所以面积以速度的关系就反过来了。超音速气流通过扩张通道时才会加速。

 

历史上，瑞典工程师拉瓦尔在研究冲击式涡轮的时候，采用收缩扩张的管道，成功让气流从亚音速加速到了超音速。于是，这种管道就被称为拉瓦尔喷管。

 

再来看看不可压和非定常的关系。这是不可压连续方程： 在推到它时，并没有假设定常流动。所以这个三维方程包括它的一维形式，对定常和非定常都成立的。

比如这个模型中，不可压时，流体密度不变，所以容腔内的流体质量保持不变，于是可知那一瞬间进出口的流量相等，可以说，单看总流量的话不可压缩流动只能是定常的。

 

接下来我们看一个流动的例子，假设有一辆行驶中的汽车缺了一块玻璃，而其余各处密封都完好不漏气。

 

分前窗侧，窗和后窗三种情况来考虑。空气是流进来还是流出去？从经验判断，前窗缺玻璃时，气体流入；后窗缺玻璃时气体流出。是这样吗？汽车的运动速度不高，属于不可压缩流动，可以用不可压缩连续方程来判断这个问题。只有一个开口，无论开口朝什么方向，流体都应该是不进也不出。虽然这似乎和感觉不同，但这就是连续方程给出的结果。那为什么坐在窗子边会有很大的风吹进来呢？这其实是流动的非定常性造成的，因为非定常性缺口有可能一半流出一半流入。

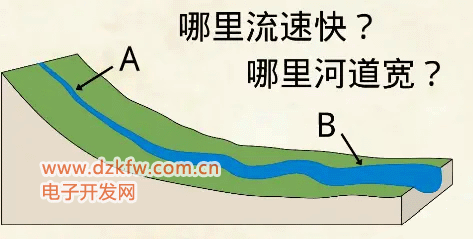
我们再来看一个河流的例子。假设这是一条没有支流的河上游，坡度大，下游坡都想那么在图中的A点和B点哪里流速快呢？这个很好判断坡度大的地方流速快。那么哪里河道宽呢？

 

这个可以用连续方程来判断流速小的地方需要的横截面积大，一般河面会宽。所以在这个例子中，流体的横截面积是由流体速度决定的。

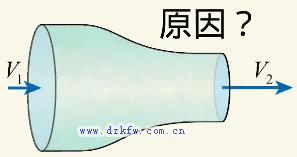
对于封闭管道内的流动横截面积是由管道决定的。看来似乎面积的收缩是流体加速的原因了。

 

然而很显然，流体遵从牛顿定律加速一定是受到了驱动力的作用。粗的地方压力高，细的地方压力低。流体微团流经收缩通道时，是从压力高的地方流向压力低的地方，相当于微团背后的压力大于前胸的压力，被推着加速前进，这就是驱动力了。所以流体加速是压力差的驱动造成的。